|
[Павлов Д.С.] <Математический алгоритм построения
геологических разрезов> [оглавление]
Общепринято (Marshak, Mitra, 1988, Groshong, 1999 и др.), что
самым простым способом построения стратоизогипс является следующий. На
геологической карте находим точки, в которых пересекаются геологические границы
и линии горизонталей. В них определены все параметры, необходимые для
построения стратоизогипс. В самом простейшем случае достаточно лишь соединить
эти точки прямыми линиями. Причем линию следует проводить через точки с
одинаковыми координатами Z и Т. Результирующая в этом случае стратоизогипса
будет описывать поведение Т-той границы на уровне высотной отметки Z. Теперь
рассмотрим, как можно построить стратоизогипсы, пользуясь другими типами
структурной информации.
Положение границы слоя на интересующей нас высоте можно получить
также с помощью имеющихся элементов залегания. Элементы залегания позволяют,
имея одну стратоизогипсу, определить, расстояние на карте до стратоизогипсы с
интересующей нас высотой. Решение такой задачи сводится к уравнению:

Поскольку сами линии стратоизогипс, которые получены с помощью
тех или иных способов, определяют элемент залегания в области между ними, то
они могут быть использованы для нахождения дополнительных стратоизогипс путем
интерполирования между известными значениями. Рассмотрим, например, случай,
представленный на рисунке 3.6.
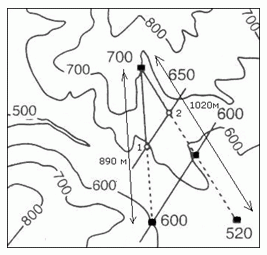 |
| Рисунок 3.6. Нахождение стратоизогипсы по известным точкам поверхности
напластования (Groshong, 1999). |
В задаче, изображенной на рисунке 3.6, известно положение трех
точек на одной геологической границе. То есть их координаты (X,Y) на карте и
высота (координата Z). Это точка с отметкой 700 м, нижняя точка с отметкой 600
м и точка, находящаяся на высоте 520 м. Надо найти положение стратоизогипсы для
высоты 650 м.
Сначала из пропорции находим вторую точку с отметкой 600 м.
Найденную точку соединяем прямой линией с уже имеющейся точкой с такой же
высотной отметкой, получаем стратоизогипсу для 600 м. Затем из подобия
треугольников находим искомую стратоизогипсу. Математический аппарат
необходимый для решения весьма прост:

Найдем расстояние до точки 1: D1 = 890*(700-650)/100 = 445м.
Найдем расстояние до точки 2: D2 = 1020*(700-650)/100 = 510м.
Обе рассмотренные формулы оперируют тангенсом угла падения, а
также вертикальной и горизонтальной составляющими расстояния в трехмерном
пространстве. Все эти величины элементарно определяются через координаты точек,
поэтому перевести их в подходящую форму для использования в алгоритме не
составит большого труда.
Также для нахождения положения границ может быть использована
мощность слоев (см. рисунок 3.7). К примеру, мы знаем (из тех или иных
источников) вертикальную мощность слоя 2 и где проходит его верхняя граница, то
есть, имеем систему стратоизогипс для его кровли. Если вертикальная мощность
слоя постоянна, то подошва слоя описывается такой же системой стратоизогипс, за
исключением того, что их высотная отметка будет меньше на значение вертикальной
мощности (Hv) слоя 2.
 |
| Рисунок 3.7.Нахождение стратоизогипс с помощью истинной и вертикальной
мощностей. Точками обозначены пересечения стратоизогипс с плоскостью разреза. |
Для подобных построений также может быть использованы сведения
об истинной мощности (H). Достаточно вычислить вертикальную мощность по
следующей формуле:

Угол падения может быть либо взят из элемента залегания, если
таковой имеется, либо вычислен из координат стратоизогипс, характеризующих
кровлю слоя 2 на рисунке 3.7 (жирные точки).
Мощности могут быть известны нам как из прямых замеров в
обнажениях, так и из бурового журнала. Проанализировав указанные выше формулы,
можно утверждать, что разнообразные вычисления в данном ключе, сводятся к
решению треугольников в координатной форме. Очевидно, не составит также труда
пересчитать высоты стратоизогипс и при линейно изменяющейся мощности, составив
пропорцию. Также решаемы и более сложные случаи. В конечном счете, множество
стратоизогипс увеличивается при поступлении дополнительных данных о положении
границ на глубине. Это положение означает, что можно бесконечно развивать
систему за счет появления новых способов нахождения стратоизогипс. С
накоплением данных, характеризующих математическую модель структуры, повышается
ее детальность.
[назад] [оглавление] [далее]
| 
