[Павлов Д.С.] <Математический алгоритм построения геологических разрезов> [оглавление]

3.4.1. Стратоизогипсы как основа математической модели геологической структуры

При построении геологического профиля главная задача заключается в том, чтобы узнать положение границ на глубине (в плоскости разреза), то есть определить координату Z точек границы. На карте же мы располагаем лишь координатами X и Y и лишь в некоторых точках поверхности напластования можем сказать о Z составляющей. Последняя однозначно определена в точках, где геологические границы и горизонтали пересекаются. Чтобы выяснить, как слой ведет себя на глубине, прибегают к вспомогательным построениям линий стратоизогипс, суть которых заключается в интерполяции поведения поверхности слоя на интервалах между точками, для которых известны все координаты.

Стратоизогипсы показывают нам, как ведет себя поверхность пласта. В случае, когда складка имеет цилиндрическую форму и горизонтальный шарнир, стратоизогипсы будут расположены параллельно друг другу и шарниру складки. В случае конической формы при тех же условиях - будут расположены веерообразно. В обоих случаях стратоизогипсы будут прямыми линиями, отстоящими друг от друга на расстояние, которое зависит от того, на сколько плавно изменяются углы падения на крыльях складок. Если в поперечном срезе замок складки имеет параболическую форму, то расстояние между стратоизогипсами будет изменяться по мере удаления от следа осевой плоскости складки. Если же сечение представляет собой нечто наподобие коробки, то расстояние между стратоизогипсами будет одинаковым в пределах тех участков складки, где залегание слоев моноклинально.

Линия стратоизогипсы не обязательно должна быть прямой, хотя часто это именно так. Представим складку, похожую по форме на седловину. Такую структуру можно получить в результате двух этапов деформации, направленных перпендикулярно друг другу. В этом случае стратоизогипса будет кривой. Также легко представить такую структуру, сравнив ее с рельефом. Если представить, что поверхность двух возвышенностей (горок) - это поверхность пласта, то изогипса для горок будет стратоизогипсой для пласта.

Следует проявлять большую осторожность при интерполяции, поскольку точки, найденные в результате пересечения линий геологических границ с линиями горизонталей, можно соединить по-разному. И в зависимости от того, как они будут соединены, определятся правильность построений.

На рисунке 3.5 представлены два возможных способа проведения системы изогипс по набору точечных данных для поверхности, к которой принадлежат эти точки. Как мы видим, в результате имеем две абсолютно непохожие картины. Избежать неоднозначности можно только в том случае, если использовать весь арсенал данных, находящийся в распоряжении геолога. В частности, для представленной на рисунке 3.5 структуры, из геологической записки известно, что в целом все структуры простираются с юго-запада на северо-восток, поэтому предпочтительным будет вариант a).

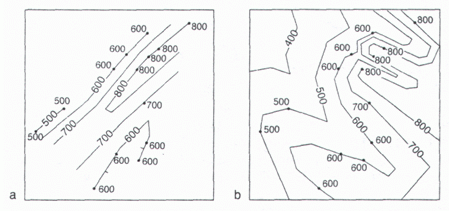Рисунок 3.5. Два возможных варианта (a и b) проведения линий равных значений.

Из выше сказанного следует, что процесс интерполяции между точечными данными не следует автоматизировать полностью, поскольку это может привести к серьезным ошибкам. Можно автоматизировать лишь частично в тех случаях, когда не может быть двоякого толкования. Например, смело можно соединить две точки линией, если они получены посредством общей пары граница-горизонталь в результате пересечения двух соответствующих линий. Принятие решения - соединять полученный отрезок с точкой пересечения имеющей те же значения высоты (Z) и индекса границы (Т) или нет - следует оставить на совесть геолога-пользователя.

Главное значение стратоизогипс заключается в том, с их помощью мы получаем модель структуры в геологическом пространстве(!), то есть в пространстве {X,Y,Z,T} При графических построениях, возможно, это не столь важно, тогда как при использовании персонального компьютера и численного описания стратоизогипс, мы может сохранить эту модель в файле и использовать ее повторно, добавляя вновь поступившие данные. Причем эта модель может быть использована не только для различных структурно-геологических целей, но и в других областях геологической науки. Например, можно использовать эту модель в качестве пространственного каркаса (геологической системы координат определенной структуры, если так можно выразиться), на котором отобразить имеющиеся данные, скажем, о химическом составе пород и проанализировать распределение тех или иных элементов в изучаемой геологической структуре. Автор полагает, что каждый геолог без труда найдет огромное количество способов применений такой модели в своих исследованиях.

Таким образом, стратоизогипсы являются ключевыми объектами математической модели геологической структуры. Выясним, как свести к этому единому представлению разнородные структурные данные.

[назад] [оглавление] [далее]