Взвешенные в воде мельчайшие частицы участвуют в беспорядочном и очень оживленном
движении. Его исследовал Р.Броун в 1827 г., и в честь ученого
оно получило название броуновского. Однако его удовлетворительное объяснение
отсутствовало вплоть до 1905 г., когда А.Эйнштейн опубликовал
свое математическое описание этого процесса, которое можно считать началом
стохастического моделирования природных явлений. Первая
математически строгая теория броуновского движения построена
Н.Винером в 1918 г. С того момента у него появился синоним:
"винеровский процесс".
С точки зрения математики броуновское движение - непрерывный
гауссовский случайный процесс 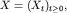 X0=0, с нулевым средним и дисперсией DXt=t.
Автокорреляционная функция его приращений -
X0=0, с нулевым средним и дисперсией DXt=t.
Автокорреляционная функция его приращений -
 -функция Дирака, что означает полное
отсутствие
корреляций в последовательных значениях приращений величины Xt и
постоянство спектра на всех частотах ( -функция Дирака, что означает полное
отсутствие
корреляций в последовательных значениях приращений величины Xt и
постоянство спектра на всех частотах (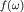 =const, =const,  -
частота).
Спектр такого вида часто называется "белым шумом" и успешно
применяется для моделирования многих климатических и гидрологических процессов.
Однако попытка его использования для объяснения эффекта Харста потерпела неудачу:
суммарный расход воды в этом случае приводит к уже упомянутой зависимости
Q~t0.5. Не спасает положения и применение случайных процессов с
конечным, не нулевым, как в винеровском процессе, временем корреляции:
В.Феллером доказано, что и в этом случае получается та же
зависимость4. -
частота).
Спектр такого вида часто называется "белым шумом" и успешно
применяется для моделирования многих климатических и гидрологических процессов.
Однако попытка его использования для объяснения эффекта Харста потерпела неудачу:
суммарный расход воды в этом случае приводит к уже упомянутой зависимости
Q~t0.5. Не спасает положения и применение случайных процессов с
конечным, не нулевым, как в винеровском процессе, временем корреляции:
В.Феллером доказано, что и в этом случае получается та же
зависимость4.
А.Н.Колмогоров в 1940 г. впервые рассмотрел случайные процессы
с дисперсией DXt=t2H,
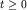 , , 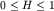 и назвал их спиралями
Винера5. Так появилось
обобщение винеровского процесса, которое впоследствии развивалось
Б.Мандельбротом6. и назвал их спиралями
Винера5. Так появилось
обобщение винеровского процесса, которое впоследствии развивалось
Б.Мандельбротом6.
Непрерывный гауссовский случайный процесс 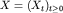 называется
фрактальным броуновским движением
с показателем Харста H, если дисперсия
этого процесса следует соотношению
DXt=t2H, t - время, 0<H<1. называется
фрактальным броуновским движением
с показателем Харста H, если дисперсия
этого процесса следует соотношению
DXt=t2H, t - время, 0<H<1.
Автокорреляционная функция приращений фрактального броуновского движения затухает
по степенному закону (характерное время корреляции этого процесса бесконечно),
а его спектр при низких частотах следует соотношению
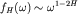 .
Другими словами, этот процесс имеет бесконечную память. .
Другими словами, этот процесс имеет бесконечную память.
При 0.5<H<1 фрактальный шум называется
"черным шумом".
Его спектральная плотность имеет неограниченный пик на нулевой
частоте.
Случайные процессы со спектральной плотностью 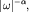 где где
 принимает значения от 0.8 до 1.4, также называют
фликкер-шумом
(от англ. flicker - мерцание, трепетание,
дрожание, короткая вспышка). Такой шум характерен для
транзисторов, речи и других
источников звука, потока автомобилей на шоссе, землетрясений и гроз; нормальный
период сердцебиения человека имеет флуктуации, спектральная плотность которых
изменяется по этому же закону. принимает значения от 0.8 до 1.4, также называют
фликкер-шумом
(от англ. flicker - мерцание, трепетание,
дрожание, короткая вспышка). Такой шум характерен для
транзисторов, речи и других
источников звука, потока автомобилей на шоссе, землетрясений и гроз; нормальный
период сердцебиения человека имеет флуктуации, спектральная плотность которых
изменяется по этому же закону.
Подчеркнем, что фликкер-шум можно считать "черным шумом" только при
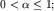 при при 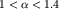 фликкер-шум -
нестационарный процесс. фликкер-шум -
нестационарный процесс.
Если использовать для моделирования расходов Нила процесс фрактального броуновского
движения, то соответствующий показатель Харста равен 0.7. Таким образом, эффект
Харста получает математическую интерпретацию: колебания стока Нила - случайный
процесс с бесконечной памятью. Однако эта аппроксимация - формальна, так как нет
ответа на главный вопрос: какие законы физики ответственны за эффект Харста?
Чтобы объяснить эффект, воспользуемся результатами
стохастического моделирования
колебания речного стока в паводочный период, выполненного на кафедре гидрологии
суши географического факультета
МГУ7. На основе материала
многолетних наблюдений
за стоком более 50 рек различных регионов мира получены статистические
закономерности колебаний паводочного стока и разработана
стохастическая (вероятностная) модель этого
процесса. Она основана на следующей аппроксимации расхода воды во времени
(гидрографа):
где S - число паводочных пиков,
t1,...,tS - даты прохождения максимальных
расходов воды, Q1,...,QS - значения этих
максимальных расходов, самостоятельно формируемых каждым паводком и накладывающихся
на спад предыдущих, а 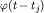 -
функция формы паводка, определяющая его динамику
( -
функция формы паводка, определяющая его динамику
(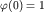 ). ).
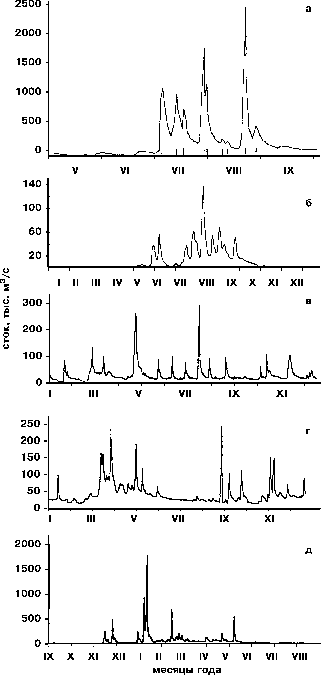
| Рис. 3. Типичные гидрографы рек с паводочным режимом.
а - Ченчон (г.Анджу, КНДР, 1957 г.);
б - Чита (с.Бургень, Читинская обл., 1957 г.);
в - Ломница (с.Перевозец, Украинские Карпаты, 1981 г.);
г - Гумиста (пос.Ачадара, Черноморское побережье Кавказа, 1980 г.);
д - Себау (пос.Баглия, Алжир, 1971-1972 гг.).
Отчетливо видна экспоненциальная форма спада паводка горных рек (в,г,д), вследствие
чего эффект Харста в паводочном режиме отсутствует.
|
Модель апробирована для рек Ченчон у г.Анджу (Северная Корея), Ломницы
(Украинские Карпаты), Читы, для многих рек бассейна Амура и др.
Для нас очень важно, что результаты упомянутых исследований доказывают:
распределения вероятностей паводочных пиков и дат их
прохождения достаточно хорошо соответствуют
распределению Пуассона, с одним и тем же параметром, который
не зависит
от времени. В последние годы этот подход широко используется для описания
последовательностей прохождения различных синоптических ситуаций, определяющих
условия формирования стока и выпадения осадков. Таким образом, правомерна постановка
задачи об определении спектра такого случайного процесса, как сток Q(t).
О подробностях нахождения корреляционной функции и
спектра импульсного случайного процесса (этот процесс случайный, так как максимальные
расходы, происходящие в случайные моменты времени
пуассоновского потока событий, сами являются случайными
величинами) любознательный читатель сможет узнать в других
работах8.
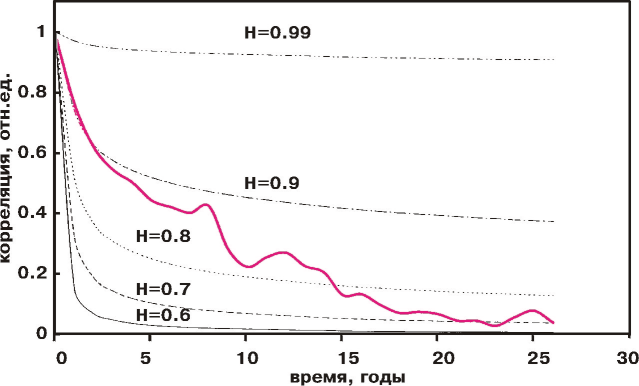
| | Рис. 4. Корреляционная функция среднегодовых величин стока Нила
(цветная линия) и корреляционные функции фрактального броуновского движения,
соответствующие разным значениям показателя Харста.
|
Оказалось, что характер спектра существенно зависит от функции формы паводка,
точнее от того, как он спадает. Так, для горных рек это происходит очень быстро,
поэтому уместна аппроксимация экспонентой 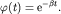 В этом случае спектр процесса
В этом случае спектр процесса 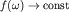 при
при 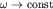 и эффект Харста у паводочного режима
отсутствует. Напротив, при медленном спадании паводка, когда оправдана аппроксимация
медленно меняющейся функцией, например и эффект Харста у паводочного режима
отсутствует. Напротив, при медленном спадании паводка, когда оправдана аппроксимация
медленно меняющейся функцией, например 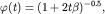 спектр
спектр 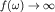 при при
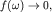 явление Харста характерно. явление Харста характерно.
Механизм формирования паводочного шлейфа (чрезвычайной распластанности гидрографа
стока) характерен для больших рек за счет продолжительного времени бассейнового
добегания и за счет задержки воды в почвогрунтах. Продолжительный же спад
воды - фактор усиления корреляции между расходами воды в разные моменты времени.
Таким образом, возможная причина эффекта Харста в паводках Нила - их медленный спад
в период отсутствия дождей.
4Feller W.// Ann. Math. Statist. 1951. V.22.
P.427-432.
5Колмогоров А.Н.//ДАН. 1940. Т.26. N2. С.115-118.
6Mandelbrot B.B., Ness J.W. van//SIAM Review. 1968.
V.10. N4. P.422-437.
7Христофоров А.В., Круглова Г.В., Самборский Т.В.
Стохастическая модель колебаний речного стока в паводочный период. М., 1998.
8Рытов С.М. Случайные процессы. М. 1976.;
Малахов А.Н.//Радиотехника и электроника. 1959. Т.4. Вып.1. N54. С.54-62.
Назад | Вперед
|

