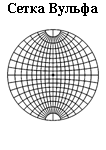|
  Сетки Вульфа, сетки Федорова и сетки Болдырева
17.09.2004 |
Я.В. Кучериненко/Геологический факультет МГУ
Представленные сетки применяются для работы со стереографическими проекциями, а именно,
для нанесения проекций направлений исходя из их сферических координат, измерения углов между
направлениями, плоскостями и ряда других задач. Наиболее известны сетки Вульфа.
Сетки Болдырева и сетки Фёдорова представляют скорее исторический, чем практический интерес,
однако все представленные сетки выполнены с высоким качеством и в разных вариантах,
так, что при желании их практического использовани . . .
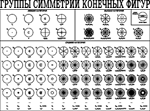 Таблица групп симметрии конечных фигур
17.09.2004 |
Я.В. Кучериненко/Геологический факультет МГУ
Плакаты А0, и А3.
На плакате показаны стереографические проекции элементов симметрии,
символы Шёнфлиса и символы Браве в их учебном варианте, максимально отражающем строение групп.
Таблица разделена на три ячейки по категориям: низшую (8 групп), высшую (7 групп) и среднюю
(13 счётных серий групп симметрии).
Таблица содержит как группы, описывающие симметрию кристаллов (их всего 32), так и группы,
не допускающие решёточное строение описываемого объекта, содержащие оси . . .
 32 класса симметрии кристаллов
17.09.2004 |
Я.В. Кучериненко/Геологический факультет МГУ
Плакаты А0, А3, А4 .
На плакате показаны стереографические проекции элементов симметрии; даны обозначения Шёнфлиса;
международные обозначения (символы Германа-Могена), как сокращённые, так и полные; символы Браве,
в том числе учебные. Все 32 группы симметрии разделены на
категории по соотношениям между
a, b, c (отрезки координатной системы) и, более детально, на сингонии по соотношениям между
. . .
 Таблица наиболее типичных координационных полиэдров
17.09.2004 |
Я.В. Кучериненко/Геологический факультет МГУ
Рисунок формата А4 при 150 dpi.
При составлении таблицы использовалась книга А.Уэллса "Структурная неорганическая химия" Т.1-3, 1987,
а также программа Balls&Sticks v.1.47. Автор заинтересован в вашей информации, какие на ваш взгляд
полиэдры можно было бы добавить к таблице. Обязательное условие: этот полиэдр должен присутствовать
хотя бы в одной реально существующей структуре кристалла. . . .
|
