Next: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Up: Приложение
Previous: Приложение
Contents: Содержание
Вопросы криптографии и секретных систем открывают возможность
для интересных применений теории связи.
В настоящей статье развивается теория секретных систем.
Изложение
ведется в теоретическом плане и имеет своей целью дополнить
положения, приводимые в обычных работах по
криптографии.
В этих работах детально
изучаются многие стандартные типы кодов и
шифров, а также способы их
расшифровки. Мы будем иметь дело с общей математической структурой
и свойствами секретных систем.
Наше изложение будет ограничено в нескольких отношениях.
Во-первых, имеются три общих типа секретных систем:
1) системы
маскировки, которые включают применение таких методов, как
невидимые чернила, представление сообщения в форме безобидного
текста или маскировки криптограммы, и другие методы, при
помощи которых факт наличия сообщения скрывается от противника;
2) тайные системы (например, инвертирование речи), в которых для
раскрытия сообщения требуется специальное оборудование;
3) ``собственно'' секретные системы, где
смысл сообщения скрывается
при помощи шифра, кодаи т.д., но само существование
сообщения не скрывается и предполагается, что противник обладает любым
специальным оборудованием, необходимым для перехвата
и записи переданных сигналов. Здесь будет рассмотрен только
третий тип систем, так как системы маскировки представляют в
основном психологическую проблему, а тайные системы --
техническую проблему.
Во-вторых, наше изложение будет ограничено случаем
дискретной информации, где сообщение,
которое должно быть
зашифровано, состоит из последовательных дискретных
символов, каждый из которых выбран из некоторого конечного
множества. Эти символы могут быть буквами или словами некоторого
языка, амплитудными уровнями ``квантованной'' речи или
видеосигнала и т.д., но главное ударение будет сделано на
случае букв.
Статья делится на три части. Резюмируем теперь кратко
основные результаты исследования. В первой части излагается
основная математическая структура
секретных систем. В теории
связи считается, что язык может рассматриваться как некоторый
вероятностный процесс, который создает дискретную
последовательность символов в соответствии с некоторой системой
вероятностей. С каждым языком связан некоторый параметр 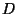 ,
который можно назвать избыточностью этого языка.
Избыточность
измеряет в некотором смысле, насколько может быть уменьшена
длина некоторого текста в данном языке без потери какой-либо
части информации. Простой пример: так как в словах английского
языка за буквой ,
который можно назвать избыточностью этого языка.
Избыточность
измеряет в некотором смысле, насколько может быть уменьшена
длина некоторого текста в данном языке без потери какой-либо
части информации. Простой пример: так как в словах английского
языка за буквой 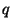 всегда следует только буква всегда следует только буква  , то , то  может быть
без ущерба опущена. Значительные сокращения в английском языке
можно осуществить, используя его статистическую структуру,
частую повторяемость определенных букв или слов, и т.д.
Избыточность играет центральную роль в изучении
секретных систем. может быть
без ущерба опущена. Значительные сокращения в английском языке
можно осуществить, используя его статистическую структуру,
частую повторяемость определенных букв или слов, и т.д.
Избыточность играет центральную роль в изучении
секретных систем.
Секретная система определяется
абстрактно как некоторое множество отображений одного пространства
(множества
возможных сообщений) в другое пространство (множество возможных
криптограмм). Каждое конкретное отображение из этого
множества соответствует способу шифрования при помощи
конкретного ключа.
Предполагается, что отображения являются взаимнооднозначными,
так что если известен ключ, то в результате процесса
расшифровки возможен лишь единственный ответ.
Предполагается далее, что
каждому ключу (и, следовательно,
каждому отображению)
соответствует некоторая априорная
вероятность -- вероятность выбрать этот ключ. Аналогично
каждому возможному сообщению соответствует априорная
вероятность, определяемая задающим сообщение вероятностным
процессом. Эти вероятности различных ключей и сообщений являются
фактически априорными вероятностями для шифровальщика
противника и характеризуют его априорные знания относительно
интересующей его проблемы.
Чтобы использовать такую секретную систему, сначала
выбирается некоторый ключ
и посылается в точку приема. Выбор
ключа определяет конкретное отображение из множества
отображений, образующих систему. Затем выбирается сообщение и с
помощью отображения, соответствующего выбранному ключу, из этого
сообщения формируется криптограмма.
Эта криптограмма передается
в точку приема по некоторому каналу и может быть перехвачена
противником.
На приемном конце с помощью отображения, обратного выбранному,
из криптограммы восстанавливают первоначальное сообщение.
Если противник перехватит криптограмму, он может с ее
помощью сосчитать апостериорные
вероятности различных
возможных сообщений и ключей, которые могли быть
использованы для составления такой криптограммы. Это
множество апостериорных вероятностей образует его сведения о
ключах и сообщениях после перехвата. ``Сведения'', таким образом,
представляют собой некоторое множество предположений, которым
приписаны вероятности. Вычисление апостериорных вероятностей
является общей задачей расшифровки.
Проиллюстрируем эти понятия простым примером. В шифре
простой
подстановки со случайным ключом имеется  отображений,
соответствующих отображений,
соответствующих  способам, которыми мы можем заменить 26
различных букв.
Все эти
способы равновозможны, и поэтому каждый имеет априорную
вероятность способам, которыми мы можем заменить 26
различных букв.
Все эти
способы равновозможны, и поэтому каждый имеет априорную
вероятность  Если такой шифр применяется к ``нормативному
английскому языку'' и предполагается, что шифровальщик
противника не знает ничего об источнике сообщений, кроме того,
что он создает английский текст, то априорными вероятностями
различных сообщений из Если такой шифр применяется к ``нормативному
английскому языку'' и предполагается, что шифровальщик
противника не знает ничего об источнике сообщений, кроме того,
что он создает английский текст, то априорными вероятностями
различных сообщений из 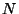 букв являются просто их относительные
частоты в нормативном английском тексте. букв являются просто их относительные
частоты в нормативном английском тексте.
Если противник перехватил такую криптограмму из 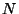 букв,
его апостериорные вероятности изменятся. Если букв,
его апостериорные вероятности изменятся. Если 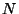 достаточно
велико (скажем, 50 букв), имеется обычно единственное сообщение
с апостериорной вероятностью, близкой к единице, в то время как
все другие сообщения имеют суммарную вероятность, близкую к
нулю. Таким образом, имеется, по существу, единственное
``решение'' такой криптограммы. Для меньших достаточно
велико (скажем, 50 букв), имеется обычно единственное сообщение
с апостериорной вероятностью, близкой к единице, в то время как
все другие сообщения имеют суммарную вероятность, близкую к
нулю. Таким образом, имеется, по существу, единственное
``решение'' такой криптограммы. Для меньших 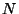 (скажем, (скажем,
 ) обычно найдется много сообщений и ключей, вероятности которых
сравнимы, и не найдется ни одного сообщения и ключа с вероятностью,
близкой к единице. В этом случае ``решение'' криптограммы
неоднозначно. ) обычно найдется много сообщений и ключей, вероятности которых
сравнимы, и не найдется ни одного сообщения и ключа с вероятностью,
близкой к единице. В этом случае ``решение'' криптограммы
неоднозначно.
В результате рассмотрения секретных систем, которые могут
быть представлены как совокупность отображений одного множества
элементов в другое, возникают две естественные операции
комбинирования, производящие из двух данных систем третью.
Первая операция комбинирования
называется операцией ``умножения''
(произведением) и соответствует зашифровке сообщения
с помощью системы  с последующей зашифровкой полученной криптограммы
с помощью системы с последующей зашифровкой полученной криптограммы
с помощью системы  , причем ключи , причем ключи  и и  выбираются независимо.
Полный результат этой операции представляет собой секретную систему,
отображения которой состоят из всех произведений (в обычном смысле
произведений отображений) отображений из выбираются независимо.
Полный результат этой операции представляет собой секретную систему,
отображения которой состоят из всех произведений (в обычном смысле
произведений отображений) отображений из  на отображения из на отображения из  .
Вероятности результирующих отображений являются произведениями
вероятностей двух исходных отображений. .
Вероятности результирующих отображений являются произведениями
вероятностей двух исходных отображений.
Вторая операция
комбинирования является ``взвешенным
сложением'':

Она представляет собой следующее. Сначала делается
предварительный выбор, какая из систем  или или  будет
использоваться, причем система будет
использоваться, причем система  выбирается с вероятностью выбирается с вероятностью  , а
система , а
система  с вероятностью с вероятностью 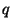 . После этого выбранная система
используется описанным выше способом. . После этого выбранная система
используется описанным выше способом.
Будет показано, что секретные системы с этими двумя
операциями комбинирования образуют, по существу, ``линейную
ассоциативную алгебру'' с единицей, -- алгебраический объект,
подробно изучавшийся математиками.
Среди многих возможных секретных систем имеется один тип
с многочисленными особыми свойствами. Этот тип назовем
``чистой'' системой.
Система является
чистой, если все ключи
равновероятны и если для любых трех отображений  , ,  , ,  из
множества отображений данной системы произведение из
множества отображений данной системы произведение

также является отображением из этого множества. То есть
зашифровка, расшифровка и снова зашифровка с любыми тремя
ключами должна быть эквивалентна зашифровке с некоторым ключом.
Можно показать, что для чистого шифра
все ключи по существу
эквивалентны -- все они приводят к тому же самому множеству
апостериорных вероятностей. Больше того, каждой криптограмме
соответствует некоторое множество сообщений
(``остаточный
класс''), из которых могла бы получиться эта криптограмма, а
апостериорные вероятности сообщений в этом классе
пропорциональны априорным вероятностям. Вся информация, которую
противник получил бы в результате перехвата криптограммы,
заключается в установлении
остаточного класса.
Многие из обычных
шифров являются чистыми системами, в том числе простая
подстановка со случайным ключом. В этом случае остаточный класс
состоит из всех сообщений с таким же набором буквенных
повторений, как в перехваченной криптограмме.
По определению,
две системы
 и и  являются ``подобными'',
если существует фиксированное отображение являются ``подобными'',
если существует фиксированное отображение  (имеющее обратное (имеющее обратное
 ) такое, что ) такое, что

Если  и и  подобны, то между получающимися в результате
применения этих систем множествами криптограмм можно установить
взаимнооднозначное соответствие, приводящее к тем же самым
апостериорным вероятностям. Такие две системы аналитически
записываются одинаково. подобны, то между получающимися в результате
применения этих систем множествами криптограмм можно установить
взаимнооднозначное соответствие, приводящее к тем же самым
апостериорным вероятностям. Такие две системы аналитически
записываются одинаково.
Во второй части статьи рассматривается проблема
``теоретической секретности''. Насколько легко некоторая
система поддается раскрытию при условии, что для анализа
перехваченной криптограммы противник располагает неограниченным
количеством времени и специалистов? Эта проблема тесно связана с
вопросами связи при наличии шумов, и понятия энтропии и
неопределенности, введенные в теории связи, находят прямое
применение в этом разделе криптографии.
``Совершенная секретность'' определяется
следующими требованиями к системе. Требуется,
чтобы апостериорные вероятности
различных сообщений, полученные после перехвата
противником данной криптограммы, были бы в точности равны
априорным вероятностям тех же сообщений до перехвата. Покажем, что
``совершенная секретность'' возможна, но требует в случае
конечного числа сообщений
того жесамого числа возможных
ключей. Если считать, что сообщение создается с данной
``скоростью''  (понятие скорости будет определено позже), то
ключ должен создаваться с той же самой или с большей скоростью. (понятие скорости будет определено позже), то
ключ должен создаваться с той же самой или с большей скоростью.
Если используется секретная система с конечным ключом и перехвачены
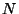 букв криптограммы, то для противника будет существовать
определенное множество сообщений с определенными вероятностями,
которые могли бы создать эту криптограмму. С увеличением букв криптограммы, то для противника будет существовать
определенное множество сообщений с определенными вероятностями,
которые могли бы создать эту криптограмму. С увеличением 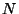 это
множество обычно сужается до тех пор, пока в конце концов не
получится единственного ``решения'' криптограммы: одно сообщение
с вероятностью, близкой к единице, а все остальные с вероятностями,
практически равными нулю. В работе определяется величина это
множество обычно сужается до тех пор, пока в конце концов не
получится единственного ``решения'' криптограммы: одно сообщение
с вероятностью, близкой к единице, а все остальные с вероятностями,
практически равными нулю. В работе определяется величина  ,
названная ненадежностью. Эта
величина измеряет (в
статистическомсмысле), насколько близка средняя криптограмма из ,
названная ненадежностью. Эта
величина измеряет (в
статистическомсмысле), насколько близка средняя криптограмма из 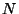 букв к единственному решению, т.е. насколько неточно известно
противнику истинное сообщение после перехвата
криптограммы из
букв к единственному решению, т.е. насколько неточно известно
противнику истинное сообщение после перехвата
криптограммы из 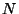 букв. Далее выводятся различные свойства
ненадежности, например: ненадежность ключа не возрастает с
ростом букв. Далее выводятся различные свойства
ненадежности, например: ненадежность ключа не возрастает с
ростом 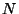 . Эта ненадежность является теоретическим показателем
секретности -- теоретическим, поскольку она позволяет противнику
дешифрировать криптограмму лишь в том случае, если он обладает
неограниченным запасом времени. . Эта ненадежность является теоретическим показателем
секретности -- теоретическим, поскольку она позволяет противнику
дешифрировать криптограмму лишь в том случае, если он обладает
неограниченным запасом времени.
В этой же части определяется функция  для некоторых
идеализированных типов шифров, называемых случайными шифрами.
С некоторыми видоизменениями эта функция может быть применена ко
многим случаям, представляющим практический интерес. Это дает
способ приближенного вычисления количества материала, который
требуется перехватить, чтобы получить решение секретной системы. для некоторых
идеализированных типов шифров, называемых случайными шифрами.
С некоторыми видоизменениями эта функция может быть применена ко
многим случаям, представляющим практический интерес. Это дает
способ приближенного вычисления количества материала, который
требуется перехватить, чтобы получить решение секретной системы.
Из подобного анализа следует, что для обычных языков и
обычных типов шифров (но не кодов) это ``расстояние
единственности'' равно приблизительно  . Здесь . Здесь  --
число, измеряющее ``объем'' пространства ключей. Если все ключи
априори равновероятны, то --
число, измеряющее ``объем'' пространства ключей. Если все ключи
априори равновероятны, то  равно логарифму числа возможных
ключей. Вводимое число равно логарифму числа возможных
ключей. Вводимое число 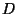 -- это избыточность языка. Оно измеряет
количество ``статистических ограничений'', налагаемых языком. Для
простой подстановки со случайным ключом наше -- это избыточность языка. Оно измеряет
количество ``статистических ограничений'', налагаемых языком. Для
простой подстановки со случайным ключом наше  равно равно
 или приблизительно 20, а или приблизительно 20, а 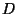 (в десятичных единицах на
букву) для английского языка равно приблизительно 0,7. Таким
образом, единственность решения достигается приблизительно
при 30 буквах. (в десятичных единицах на
букву) для английского языка равно приблизительно 0,7. Таким
образом, единственность решения достигается приблизительно
при 30 буквах.
Для некоторых ``языков'' можно
построить такие секретные
системы с конечным ключом, в которых неопределенность не
стремится к нулю при  . В этом случае противник не
получит единственного решения такого шифра, сколько бы
материала он не перехватил, и у него будет оставаться много
альтернатив с довольно большими вероятностями. Такие системы
назовем идеальными системами. В любом языке можно
аппроксимировать такую ситуацию, т.е. отсрочить приближение . В этом случае противник не
получит единственного решения такого шифра, сколько бы
материала он не перехватил, и у него будет оставаться много
альтернатив с довольно большими вероятностями. Такие системы
назовем идеальными системами. В любом языке можно
аппроксимировать такую ситуацию, т.е. отсрочить приближение
 к нулю до сколь угодно больших к нулю до сколь угодно больших 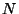 . Однако такие системы
имеют много недостатков, таких как сложность и чувствительность
к ошибкам при передаче криптограммы. . Однако такие системы
имеют много недостатков, таких как сложность и чувствительность
к ошибкам при передаче криптограммы.
Третья часть статьи посвящена ``практической секретности''.
Две системы с одинаковым объемом ключа могут быть обе разрешимы
единственным образом, когда перехвачено 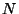 букв, но они могут
значительно отличаться по количеству времени и усилий,
затрачиваемых для получения решения. На основе анализа основных
недостатков секретных систем предлагаются методы построения
систем, для решения которых требуются большие затраты времени и
сил. Наконец, рассматривается проблема несовместимости различных
желательных качеств секретных систем. букв, но они могут
значительно отличаться по количеству времени и усилий,
затрачиваемых для получения решения. На основе анализа основных
недостатков секретных систем предлагаются методы построения
систем, для решения которых требуются большие затраты времени и
сил. Наконец, рассматривается проблема несовместимости различных
желательных качеств секретных систем.
Next: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Up: Приложение
Previous: Приложение
Contents: Содержание
|

