Next: 8. Подобные системы
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: 6. Алгебра секретных систем
Contents: Содержание
Некоторые типы шифров, такие как простая подстановка,
транспозиция с данным периодом,
система Виженера с данным периодом,
Рис. 4.
 |
система Виженера со смешанным алфавитом и т.д.
(все с равновероятными ключами), обладают некоторой
однородностью по отношению к ключу. Каков бы ни был ключ,
процессы шифрования, дешифрирования адресатом и
дешифрирования противником являются по существу теми же
самыми. Эти системы можно противопоставить системе с шифром

где  -- простая подстановка, а -- простая подстановка, а 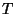 -- транспозиция с данным
периодом. В таком случае процессы шифрования и дешифрирования
адресатом или противником полностью меняются в зависимости от
того, используется подстановка или транспозиция. -- транспозиция с данным
периодом. В таком случае процессы шифрования и дешифрирования
адресатом или противником полностью меняются в зависимости от
того, используется подстановка или транспозиция.
Причина однородности таких систем лежит в групповом свойстве:
заметим, что в приведенных выше примерах однородных шифров
произведение  любых двух отображений из множества равно
третьему отображению любых двух отображений из множества равно
третьему отображению  из этого же множества. С другой
стороны, из этого же множества. С другой
стороны,  не равно какому-нибудь отображению для шифра не равно какому-нибудь отображению для шифра

который содержит только подстановки и транспозиции, но не их
произведения.
Было бы можно, таким образом, определить ``чистый'' шифр как
шифр, в котором  образуют группу. Однако это было бы слишком
сильным ограничением, так как тогда потребовалось бы, чтобы
пространство образуют группу. Однако это было бы слишком
сильным ограничением, так как тогда потребовалось бы, чтобы
пространство 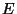 совпадало с пространством совпадало с пространством 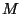 , т.е. чтобы система
была эндоморфной. Дробная транспозиция так же однородна, как
и обычная транспозиция, но она не эндоморфна. Подходящим
является следующее определение: шифр , т.е. чтобы система
была эндоморфной. Дробная транспозиция так же однородна, как
и обычная транспозиция, но она не эндоморфна. Подходящим
является следующее определение: шифр
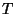 является чистым, если для
каждых является чистым, если для
каждых  имеется такое имеется такое  , что , что

и все ключи равновероятны. В противном случае шифр является
смешанным. Шифры на рис. 2 являются смешанными, а на
рис. 4 -- чистыми, если только все ключи равновероятны.
Теорема 1.
В чистом шифре операции  , отображающие
пространство сообщений в себя, образуют группу, порядок
которой равен , отображающие
пространство сообщений в себя, образуют группу, порядок
которой равен  -- числу различных ключей. -- числу различных ключей.
Так как

то каждый элемент имеет обратный. Ассоциативный закон верен,
так как это операции, а групповое свойство следует из того, что

где предполагалось, что
 для некоторого для некоторого  . .
Операция  означает шифрование сообщения с помощью
ключа означает шифрование сообщения с помощью
ключа 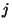 с последующим дешифрованием с помощью ключа с последующим дешифрованием с помощью ключа 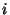 , что
приводит нас назад к пространству сообщений. Если система , что
приводит нас назад к пространству сообщений. Если система 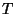 эндоморфна, т.е.
эндоморфна, т.е.  отображают пространство отображают пространство  в само себя (что
имеет место для большинства шифров, в которых и пространство
сообщений, и пространство криптограмм состоит из
последовательностей букв), и если в само себя (что
имеет место для большинства шифров, в которых и пространство
сообщений, и пространство криптограмм состоит из
последовательностей букв), и если  образуют группу и
равновероятны, то образуют группу и
равновероятны, то 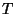 -- чистый шифр, так как -- чистый шифр, так как

Теорема 2.
Произведение двух чистых коммутирующих
шифров является чистым шифром.
Если 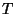 и и  коммутируют, то коммутируют, то
 для любых для любых
 при
соответствующих при
соответствующих  . Тогда . Тогда

Условие коммутирования не является, однако, необходимым для
того, чтобы произведение было чистым шифром.
Система, состоящая из одного ключа, т.е. из единственной
определенной операции  , является чистым шифром, т.е. при
единственном возможном выборе индексов имеем , является чистым шифром, т.е. при
единственном возможном выборе индексов имеем

Таким образом, разложение шифра в сумму таких простых
отображений представляет собой разложение в его сумму чистых
шифров.
Исследование примера, приведенного на рис. 4, вскрывает
некоторые свойства чистого шифра. Сообщения распадаются на
определенные подмножества, которые мы будем называть
остаточными классами, и возможные криптограммы также
распадаются на соответствующие им остаточные классы. От каждого
сообщения в любом классе к каждой криптограмме в соответствующем
классе имеется не менее одной линии и нет линий между
несоответствующими классами. Число сообщений в классе является
делителем полного числа ключей. Число ``параллельных'' линий от
сообщения 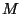 к криптограмме в соответствующем классе равно числу
ключей, деленному на число сообщений в классе, содержащем это
сообщение (или криптограмму). к криптограмме в соответствующем классе равно числу
ключей, деленному на число сообщений в классе, содержащем это
сообщение (или криптограмму).
В приложении2)
показывается, что это верно для чистых шифров и
в общем случае. Резюмируя сказанное, мы имеем
Теорема 3.
В чистой системе сообщения можно разделить
на множество ``остаточных классов''
 ,
а криптограммы --
на соответствующее множество остаточных классов ,
а криптограммы --
на соответствующее множество остаточных классов
 . Эти классы будут иметь следующие свойства: . Эти классы будут иметь следующие свойства:
1. Остаточные классы сообщений взаимно исключают друг друга
и содержат все возможные сообщения. Аналогичное утверждение
верно и для остаточных классов криптограмм.
2. Если зашифровать любое сообщение из класса  с помощью
любого ключа, то получится криптограмма из класса с помощью
любого ключа, то получится криптограмма из класса  .
Дешифрирование любой криптограммы из класса .
Дешифрирование любой криптограммы из класса  с помощью любого
ключа приводит к сообщению из класса с помощью любого
ключа приводит к сообщению из класса  . .
3. Число сообщений в классе  , скажем, , скажем,  , равно числу
криптограмм в классе , равно числу
криптограмм в классе  и является делителем и является делителем  -- числа
ключей. -- числа
ключей.
4. Каждое сообщение из класса  может быть зашифровано
в каждую криптограмму из класса может быть зашифровано
в каждую криптограмму из класса  при помощи точно при помощи точно  различных ключей. То же самое верно и для дешифрирования.
различных ключей. То же самое верно и для дешифрирования.
Смысл понятия чистый шифр (и причина для выбора такого
термина) лежит в том, что в чистом шифре все ключи являются
по существу одинаковыми. Какой бы ключ ни использовался для
заданного сообщения, апостериорные вероятности всех сообщений
будут теми же самыми.
Чтобы показать это, заметим, что два различных
ключа, примененных к одному сообщению, дадут в результате две
криптограммы из одного остаточного класса, скажем  . Поэтому эти
две криптограммы могут быть расшифрованы с помощью . Поэтому эти
две криптограммы могут быть расшифрованы с помощью  ключей в
каждое из сообщений в классе ключей в
каждое из сообщений в классе  и больше ни в какие возможные
сообщения. Так как все ключи равновероятны,
то апостериорные вероятности различных сообщений
равны и больше ни в какие возможные
сообщения. Так как все ключи равновероятны,
то апостериорные вероятности различных сообщений
равны

где 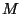 -- сообщение из класса -- сообщение из класса  , , 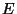 -- криптограмма из класса -- криптограмма из класса
 и сумма берется по всем и сумма берется по всем 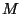 из класса из класса  . Если . Если 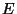 и и 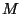 не
принадлежат соответствующим остаточным классам, то не
принадлежат соответствующим остаточным классам, то  . .
Аналогично можно показать, что набор апостериорных
вероятностей различных ключей всегда одинаков, но эти
вероятности ставятся в соответствие ключам лишь после того,
как уже использован некоторый ключ. При изменении частного ключа
это множество чисел  подвергается перестановке.
Иными словами, имеем: подвергается перестановке.
Иными словами, имеем:
Теорема 4.
В чистой системе апостериорные вероятности
различных сообщений  не зависят от выбора ключа.
Апостериорные вероятности ключей не зависят от выбора ключа.
Апостериорные вероятности ключей  образуют один и тот
же набор величин, но подвергаются перестановке в результате
различных выборов ключа. образуют один и тот
же набор величин, но подвергаются перестановке в результате
различных выборов ключа.
Грубо говоря, можно считать, что любой выбор ключа в чистом
шифре приводит к одинаковым трудностям при дешифрировании.
Поскольку различные ключи все приводят к формированию
криптограмм из одного и того же остаточного класса, то все
криптограммы из одного остаточного класса эквивалентны с точки
зрения сложности дешифрирования -- они приводят к тем же самым
апостериорным вероятностям сообщений и, если учитывать
перестановки, к тем же самым вероятностям ключей.
В качестве примера чистого шифра может служить простая
подстановка с равновероятными ключами. Остаточный класс,
соответствующий данной криптограмме 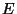 , является множеством
всех криптограмм, которые могут быть получены из , является множеством
всех криптограмм, которые могут быть получены из 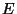 с помощью
операций с помощью
операций  . В рассматриваемом случае операция . В рассматриваемом случае операция
 сама
является подстановкой и поэтому любая подстановка переводит
криптограмму сама
является подстановкой и поэтому любая подстановка переводит
криптограмму 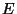 в другой член того же самого остаточного класса;
таким образом, если криптограмма представляет собой в другой член того же самого остаточного класса;
таким образом, если криптограмма представляет собой

принадлежат к тому же остаточному классу. В этом случае
очевидно, что криптограммы по существу эквивалентны. Все
существенное в простой подстановке со случайным ключом заключено
в характере повторения букв, в то время как сами буквы являются
несущественной маскировкой. В действительности можно бы
полностью обойтись без них, указав характер повторений букв в 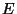 следующим образом:
следующим образом:
|
 |
Это обозначение описывает остаточный класс, но устраняет всю
информацию относительно конкретных членов этого класса; таким
образом, оно представляет как раз ту информацию, которая имеет
значение для шифровальщика противника. Это связано с одним из
методов подхода к раскрытию шифров типа простой подстановки
методом характерных слов.
В шифре типа Цезаря имеют значение
только первые разности
криптограммы по модулю 26. Две криптограммы с теми же самыми
разностями ( ) принадлежат к одному остаточному классу.
Этот шифр можно раскрыть путем простого процесса выписывания
двадцати шести сообщений из этого остаточного класса и выбора
того из них, которое имеет смысл. ) принадлежат к одному остаточному классу.
Этот шифр можно раскрыть путем простого процесса выписывания
двадцати шести сообщений из этого остаточного класса и выбора
того из них, которое имеет смысл.
Шифр Виженера с периодом 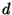 со случайным ключом представляет
собой другой пример чистого шифра. Здесь остаточный класс
сообщений состоит из всех последовательностей с теми же первыми
разностями, что и у криптограммы для букв, отстоящих на
расстояние со случайным ключом представляет
собой другой пример чистого шифра. Здесь остаточный класс
сообщений состоит из всех последовательностей с теми же первыми
разностями, что и у криптограммы для букв, отстоящих на
расстояние 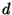 . Для . Для  остаточный класс определяется с помощью
равенств остаточный класс определяется с помощью
равенств

где  --
криптограмма, а --
криптограмма, а  является любым
сообщением является любым
сообщением 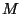 в соответствующем остаточном классе. в соответствующем остаточном классе.
В транспозиции с периодом 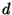 со
случайным ключом остаточный
класс состоит из всех способов расстановок символов криптограммы,
в которых никакое со
случайным ключом остаточный
класс состоит из всех способов расстановок символов криптограммы,
в которых никакое  не выдвигается из своего блока длины не выдвигается из своего блока длины 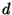 и любые два
и любые два  с расстоянием с расстоянием 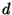 остаются на таком же расстоянии.
Это используется для раскрытия шифра следующим образом:
криптограмма записывается в виде последовательных блоков длины остаются на таком же расстоянии.
Это используется для раскрытия шифра следующим образом:
криптограмма записывается в виде последовательных блоков длины 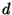 один под другим, как показано ниже (для
один под другим, как показано ниже (для 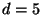 ) )

Затем столбцы переставляются до тех пор, пока не получится
осмысленный текст. После того как криптограмма разбита на
столбцы, оставшейся существенной информацией является только
остаточный класс криптограммы.
Теорема 5.
Если шифр 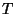 -- чистый, то -- чистый, то
 ,
где ,
где  -- любые два отображения из -- любые два отображения из 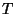 . Обратно, если это
выполняется для любых принадлежащих шифру . Обратно, если это
выполняется для любых принадлежащих шифру  , то шифр , то шифр 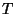 является чистым.
является чистым.
Первая часть этой теоремы следует, очевидно, из определения
чистого шифра. Чтобы доказать вторую часть, заметим сначала,
что если
 , то , то
 является
отображением из является
отображением из 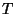 . Остается показать, что все ключи равновероятны.
Имеем . Остается показать, что все ключи равновероятны.
Имеем
 и и

Слагаемое в стоящей слева сумме с  дает дает  .
Единственным слагаемым с .
Единственным слагаемым с  в правой части является
в правой части является  . Так
как все коэффициенты неотрицательны, то отсюда следует, что . Так
как все коэффициенты неотрицательны, то отсюда следует, что

То же самое рассуждение остается справедливым, если 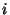 и и 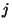 поменять местами. Следовательно,
поменять местами. Следовательно,

и 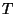 -- чистый шифр. Таким образом,
условие -- чистый шифр. Таким образом,
условие
 можно
было бы использовать в качестве другого определения чистого
шифра.
можно
было бы использовать в качестве другого определения чистого
шифра.
Next: 8. Подобные системы
Up: Часть I. МАТЕМАТИЧЕСКАЯ СТРУКТУРА СЕКРЕТНЫХ
Previous: 6. Алгебра секретных систем
Contents: Содержание
|

