Next: 7.5. Условия задач олимпиад
Up: 7. Олимпиады по криптографии
Previous: Ответы к упражнению.
Contents: Содержание
7.4. Многоалфавитные шифры замены с периодическим ключом
Рассмотрим 30-буквенный алфавит русского языка:
|
АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯ.
|
В этом алфавите отсутствуют буквы  , Й и
Ъ, что
практически не ограничивает возможностей по составлению открытых
сообщений на русском языке. В самом деле, замена буквы , Й и
Ъ, что
практически не ограничивает возможностей по составлению открытых
сообщений на русском языке. В самом деле, замена буквы  на
букву Е, буквы Й - на букву И, а буквы
Ъ - на букву Ь позволяет понять
смысл открытого сообщения, написанного с использованием этого
алфавита. на
букву Е, буквы Й - на букву И, а буквы
Ъ - на букву Ь позволяет понять
смысл открытого сообщения, написанного с использованием этого
алфавита.
В алфавите любого естественного языка буквы следуют друг за другом в
определенном порядке. Это дает возможность присвоить каждой букве алфавита
ее естественный порядковый номер. Так, в приведенном алфавите букве
А
присваивается порядковый номер 1, букве
О - порядковый номер 14, а букве
Ы -
порядковый номер 27. Если в открытом сообщении каждую букву
заменить ее естественным порядковым номером в рассматриваемом
алфавите, то преобразование числового сообщения в буквенное
позволяет однозначно восстановить исходное открытое сообщение.
Например, числовое сообщение 1 11 20 1 3 9 18 преобразуется в
буквенное сообщение: АЛФАВИТ.
Дополним естественный порядок букв в алфавите. Будем считать,
что за последней буквой алфавита следует его первая буква. Такой
порядок букв достигается, если расположить их на окружности в
естественном порядке по часовой стрелке. При таком расположении можно
каждой из букв присвоить порядковый номер относительно любой буквы
алфавита. Такой номер назовем относительным порядковым номером.
Заметим, что если число букв в алфавите равно  , то относительный
порядковый номер данной буквы может принимать все значения от 0 до , то относительный
порядковый номер данной буквы может принимать все значения от 0 до
 в зависимости от буквы, относительно которой он вычисляется.
Для примера рассмотрим исходный 30-буквенный алфавит русского
языка, расположенный на окружности (см. рис.). в зависимости от буквы, относительно которой он вычисляется.
Для примера рассмотрим исходный 30-буквенный алфавит русского
языка, расположенный на окружности (см. рис.).
|
 |
В этом случае порядковый номер буквы А относительно буквы А
равен 0, относительно буквы
Я он уже равен 1 и так далее, относительно
буквы Б порядковый номер
А равен 29. Значения относительных порядковых
номеров букв алфавита из  букв совпадают со значениями всевозможных
остатков от деления целых чисел на натуральное число букв совпадают со значениями всевозможных
остатков от деления целых чисел на натуральное число  . Убедитесь в
том, что порядковый номер какой-либо буквы алфавита относительно
другой буквы равен остатку от деления разности их естественных
порядковых номеров на число букв в алфавите. . Убедитесь в
том, что порядковый номер какой-либо буквы алфавита относительно
другой буквы равен остатку от деления разности их естественных
порядковых номеров на число букв в алфавите.
Обозначим символами:
 - порядковый номер буквы с естественным порядковым
номером - порядковый номер буквы с естественным порядковым
номером  относительно буквы с естественным порядковым
номером относительно буквы с естественным порядковым
номером  ; ;
 -
остаток от деления целого числа -
остаток от деления целого числа 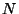 на натуральное число на натуральное число  . .
При этом справедливо равенство
 , где , где
 - число букв в алфавите. - число букв в алфавите.
Для удобства обозначим
![$N_1\mathop{\rlap{\hskip-1pt$\square$}\hbox{\rule[1mm]{1.9mm}{1pt}}}N_2=r_z(N_1-N_2)$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1218.gif) , ,
![$N_1\mathop{\rlap{\hskip-1pt$\square$}\rlap{\hskip1.2mm\hskip-1pt\rule[0.1mm]{1pt}{2.1mm}}
\rule[1mm]{2.1mm}{1pt}}N_2=r_z(N_1+\ +N_2)$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1219.gif) . Тогда
имеют место равенства: . Тогда
имеют место равенства:
![\begin{gather}
D(N_1,N_2)=N_1\mathop{\rlap{\hskip-1pt$\square$}\hbox{\rule[1mm]{...
...ip-1pt\rule[0.1mm]{1pt}{2.1mm}}
\rule[1mm]{2.1mm}{1pt}}D(N_1,N_2).
\end{gather}](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1220.gif)
Формула (8) непосредственно получается
из (7) и ее можно использовать для замены буквы с
естественным порядковым номером  на букву с естественным
порядковым номером на букву с естественным
порядковым номером  . Число . Число  называется знаком гаммы.
называется знаком гаммы.
Для уяснения введенных обозначений читателю предлагается
самостоятельно решить следующие задачи.
1. Докажите, что для любых целых  , ,  и любого
натурального и любого
натурального  справедливо равенство:
справедливо равенство:
![$ \displaystyle D(N_1,N_2)=N_1-N_2-\left[\frac{N_1-N_2}{z}\right]\cdot z
$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1221.gif) , где , где ![$ [X]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1222.gif) - целая часть
числа - целая часть
числа  (наибольшее целое число, не превосходящее числа (наибольшее целое число, не превосходящее числа 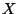 ). ).
2. Докажите равенство (8) и равенство:
![\begin{displaymath}
N_2=N_1\mathop{\rlap{\hskip-1pt$\square$}\hbox{\rule[1mm]{1.9mm}{1pt}}}D(N_1,N_2).
\end{displaymath}](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1224.gif) |
(7) |
Для зашифрования некоторого открытого сообщения, состоящего из 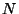 букв, с помощью указанной замены требуется
букв, с помощью указанной замены требуется 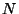 знаков гаммы: по одному
на каждую букву сообщения.
Последовательность
знаков гаммы,
необходимая для зашифрования открытого сообщения, является
ключом данного шифра. знаков гаммы: по одному
на каждую букву сообщения.
Последовательность
знаков гаммы,
необходимая для зашифрования открытого сообщения, является
ключом данного шифра.
Если последовательность
знаков гаммы имеет небольшой
(по сравнению с длиной открытого текста) период, то соответствующий
шифр называется шифром замены с периодическим ключом. Ключом такого
шифра, по существу, является отрезок гаммы, равный по длине периоду.
Число отрезков некоторой длины 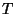 , состоящих из чисел от 0
до , состоящих из чисел от 0
до  равно равно  , так как на каждой из , так как на каждой из 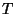 позиций
отрезка может быть любое из позиций
отрезка может быть любое из  чисел (независимо от чисел,
находящихся на других позициях). Для наглядности приведем значения чисел (независимо от чисел,
находящихся на других позициях). Для наглядности приведем значения
 при при  в зависимости от значений в зависимости от значений 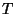 : :
|
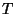 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
 |
30 |
900 |
27000 |
810000 |
24300000 |
 |
 |
|
Как видно из приведенной таблицы, число ключей рассматриваемого шифра
замены с ключом периода 10, достаточно внушительно и составляет уже
сотни триллионов. Это обстоятельство делает практически
невозможным вскрытие шифра методом перебора всех его ключей даже при
меньших значениях периода гаммы.
Для рассматриваемого шифра характерно то, что буквы
открытого текста, зашифрованные одним и тем же знаком гаммы, по
сути, зашифрованы одним и тем же шифром простой замены. Например,
ключевая таблица этого шифра простой замены при знаке гаммы,
равном 1, имеет вид:
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Э |
Ю |
Я |
|
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Э |
Ю |
Я |
А
|
|
Вторую строку этой ключевой таблицы называют алфавитом шифрования,
соответствующим данному знаку гаммы. Поскольку в рассматриваемом шифре
возможны все значения гаммы от 0 до 29, то данный шифр можно
рассматривать как 30-алфавитный шифр замены. Если каждому из этих
алфавитов поставить в соответствие его первую букву, то каждый знак
гаммы можно заменить этой буквой. В этом случае ключ рассматриваемого
шифра можно взаимнооднозначно заменить соответствующим словом в этом
же алфавите. Такой многоалфавитный шифр замены был описан
в 1585 году французом Блезом де Виженером в
его ``Трактате о шифрах'':
|
ABCDEFGHIJKLMNOPQRSTUVWXYZ
BCDEFGHIJKLMNOPQRSTUVWXYZA
CDEFGHIJKLMNOPQRSTUVWXYZAB
DEFGHIJKLMNOPQRSTUVWXYZABC
EFGHIJKLMNOPQRSTUVWXYZABCD
FGHIJKLMNOPQRSTUVWXYZABCDE
GHIJKLMNOPQRSTUVWXYZABCDEF
HIJKLMNOPQRSTUVWXYZABCDEFG
IJKLMNOPQRSTUVWXYZABCDEFGH
JKLMNOPQRSTUVWXYZABCDEFGHI
KLMNOPQRSTUVWXYZABCDEFGHIJ
LMNOPQRSTUVWXYZABCDEFGHIJK
MNOPQRSTUVWXYZABCDEFGHIJKL
NOPQRSTUVWXYZABCDEFGHIJKLM
OPQRSTUVWXYZABCDEFGHIJKLMN
PQRSTUVWXYZABCDEFGHIJKLMNO
QRSTUVWXYZABCDEFGHIJKLMNOP
RSTUVWXYZABCDEFGHIJKLMNOPQ
STUVWXYZABCDEFGHIJKLMNOPQR
TUVWXYZABCDEFGHIJKLMNOPQRS
UVWXYZABCDEFGHIJKLMNOPQRST
VWXYZABCDEFGHIJKLMNOPQRSTU
WXYZABCDEFGHIJKLMNOPQRSTUV
XYZABCDEFGHIJKLMNOPQRSTUVW
YZABCDEFGHIJKLMNOPQRSTUVWX
ZABCDEFGHIJKLMNOPQRSTUVWXY
|
Все
алфавиты шифрования относительно латинского алфавита были сведены им в
таблицу, получившую впоследствии название ее автора.
Выше приведена таблица Виженера
для современного латинского алфавита,
она состоит из списка 26 алфавитов шифрования.
Способ зашифрования с помощью таблицы Виженера заключается
в том, что первый из алфавитов соответствует алфавиту открытого
текста, а букве ключевого слова соответствует алфавит шифрования из
данного списка, начинающийся с этой буквы. Буква шифрованного текста
находится в алфавите шифрования на месте, соответствующем данной букве
открытого текста. Простота построения таблицы Виженера делает эту
систему привлекательной для практического использования. Рассмотрим
пример вскрытия многоалфавитного шифра замены с периодическим
ключом, содержащийся в рассказе Жюля Верна ``Жангада''. Вот
текст, который был получен с помощью такого типа
шифра:
|
|
С |
Г |
У |
Ч |
П |
В |
Э |
Л |
Л |
З |
Й |
Р |
Т |
Е |
П |
Н |
Л |
Н |
Ф |
Г |
И |
Н |
Б |
О |
Р |
Г |
Й |
У |
|
Г |
Л |
Ч |
Д |
К |
О |
Т |
Х |
Ж |
Г |
У |
У |
М |
З |
Д |
Х |
Р |
Ъ |
С |
Г |
С |
Ю |
Д |
Т |
П |
Ъ |
А |
Р |
|
В |
Й |
Г |
Г |
И |
Щ |
В |
Ч |
Э |
Е |
Ц |
С |
Т |
У |
Ж |
В |
С |
Е |
В |
Х |
А |
Х |
Я |
Ф |
Б |
Ь |
Б |
Е |
|
Т |
Ф |
З |
С |
Э |
Ф |
Т |
Х |
Ж |
З |
Б |
З |
Ъ |
Г |
Ф |
Б |
Щ |
И |
Х |
Х |
Р |
И |
П |
Ж |
Т |
З |
В |
Т |
|
Ж |
Й |
Т |
Г |
О |
Й |
Б |
Н |
Т |
Ф |
Ф |
Е |
О |
И |
Х |
Т |
Т |
Е |
Г |
И |
И |
О |
К |
З |
П |
Т |
Ф |
Л |
|
Е |
У |
Г |
С |
Ф |
И |
П |
Т |
Ь |
М |
О |
Ф |
О |
К |
С |
Х |
М |
Г |
Б |
Т |
Ж |
Ф |
Ы |
Г |
У |
Ч |
О |
Ю |
|
Н |
Ф |
Н |
Ш |
З |
Г |
Э |
Л |
Л |
Ш |
Р |
У |
Д |
Е |
Н |
К |
О |
Л |
Г |
Г |
Н |
С |
Б |
К |
С |
С |
Е |
У |
|
П |
Н |
Ф |
Ц |
Е |
Е |
Е |
Г |
Г |
С |
Ж |
Н |
О |
Е |
Ы |
И |
О |
Н |
Р |
С |
И |
Т |
К |
Ц |
Ь |
Е |
Д |
Б |
|
У |
Б |
Т |
Е |
Т |
Л |
О |
Т |
Б |
Ф |
Ц |
С |
Б |
Ю |
Й |
П |
М |
П |
З |
Т |
Ж |
П |
Т |
У |
Ф |
К |
Д |
Г
|
|
Догадавшись, что ключом является натуральное число, персонаж
``Жангады'', судья Жаррикес, объясняет сыну обвиняемого Маноэлю,
как был зашифрован документ: -``Давайте возьмем фразу, все равно
какую, ну хотя бы вот эту:
|
У СУДЬИ ЖАРРИКЕСА ПРОНИЦАТЕЛЬНЫЙ УМ |
А теперь я возьму наудачу какое-нибудь число, чтобы сделать из
этой фразы криптограмму. Предположим, что число состоит из трех цифр,
например, 4, 2 и 3. Я подписываю число 423 под строчкой так, чтобы
под каждой буквой стояла цифра, и повторяю число, пока не дойду до
конца фразы. Вот что получится:
|
У |
С |
У |
Д |
Ь |
И |
Ж |
А |
Р |
Р |
И |
К |
Е |
С |
А |
П |
Р |
О |
Н |
И |
Ц |
А |
Т |
Е |
Л |
Ь |
Н |
Ы |
Й |
У |
М |
|
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4 |
2 |
3 |
4
|
|
Будем заменять каждую букву нашей фразы той буквой, которая стоит после нее в
алфавите
|
АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ |
на месте, указанном цифрой. Например, если под буквой
А стоит цифра 3, вы
отсчитываете три буквы и заменяете ее буквой
Г. Если буква находится в конце
алфавита и к ней нельзя прибавить нужного числа букв, тогда отсчитывают
недостающие буквы с начала алфавита.
Доведем до конца начатую криптограмму, построенную на числе
423, и исходная фраза заменится следующей:
|
Ч |
У |
Ц |
И |
Ю |
Л |
К |
В |
У |
Ф |
К |
Н |
Й |
У |
Г |
У |
Т |
С |
С |
К |
Щ |
Д |
Ф |
И |
П |
Ю |
Р |
Я |
Л |
Ц |
Р
|
|
Но как найти числовой ключ? Подсчет, проведенный Жаррикесом,
показывает, что поиск ключа перебором всех возможных чисел, состоящих
не более чем из 10 цифр, потребует более трехсот лет. Судья пытается
наудачу отгадать заветное число.
Наступает день казни. Обвиняемого Жоама Дакосту ведут
на виселицу
Но все заканчивается благополучно. Помог счастливый случай.
Другу Жоама удается узнать, что автора криптограммы звали Ортега.
Поставив буквы О, Р, Т, Е, Г,
А над последними шестью буквами
документа и подсчитав, на сколько эти буквы по алфавиту сдвинуты
относительно букв криптограммы, судья, наконец, находит ключ к
документу:
|
исходное сообщение
|
О |
Р |
Т |
Е |
Г |
А |
|
шифрованное сообщение |
Т |
У |
Ф |
К |
Д |
Г |
|
относительный сдвиг букв |
4 |
3 |
2 |
5 |
1 |
3
|
|
Г.А.Гуревич в статье ``Криптограмма Жюля Верна''
(журнал ``Квант'' #9, 1985 г.) обращает внимание
на то, что судья прошел практически весь путь до отгадки. Будучи
уверенным, что в документе упоминается имя Жоама Дакосты, судья
строит предположение: ``Если бы строчки были разделены
на слова, то мы могли бы выделить слова, состоящие из семи букв, как и
фамилия Дакоста, и, опробуя их одно за другим, может быть и отыскали бы
число, являющееся ключом криптограммы''. Маноэль, в свою очередь,
поняв основную идею судьи, предлагает опробовать возможные
расположения слова ДАКОСТА в исходном тексте. Поскольку текст
состоит из 252 букв, то достаточно опробовать не более 246 вариантов.
В один прекрасный момент, записав над фрагментом
ЙБНТФФЕ слово ДАКОСТА, мы определили бы
последовательность цифр 5134325. Естественно предположить, что
последняя цифра 5 - начало следующего периода:
|
исходное сообщение |
... |
Д |
А |
К |
О |
С |
Т |
А |
... |
|
шифрованное сообщение |
... |
Й |
Б |
Н |
Т |
Ф |
Ф |
Е |
... |
|
относительный сдвиг букв |
... |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
...
|
|
Вместо ключа 432513 мы нашли его циклическую перестановку 513432, что
ни в коей мере не мешает расшифрованию текста. Для этого достаточно
для каждой буквы шифрованного текста
определить букву, относительно которой данная буква сдвинута на
величину соответствующей цифры ключа:
|
С |
Г |
У |
Ч |
П |
В |
Э |
Л |
Л |
З |
Й |
Р |
Т |
Е |
П |
Н |
Л |
Н |
Ф |
Г |
И |
Н |
Б |
О |
Р |
|
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
|
Н |
А |
С |
Т |
О |
Я |
Щ |
И |
Й |
В |
И |
Н |
О |
В |
Н |
И |
К |
К |
Р |
А |
Ж |
И |
А |
Л |
М
|
|
Г |
Й |
У |
Г |
Л |
Ч |
Д |
К |
О |
Т |
Х |
Ж |
Г |
У |
У |
М |
З |
Д |
Х |
Р |
Ъ |
С |
Г |
С |
Ю |
|
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
|
А |
З |
О |
В |
И |
У |
Б |
И |
Й |
С |
Т |
В |
А |
С |
О |
Л |
Д |
А |
Т |
О |
Х |
Р |
А |
Н |
Ы
|
|
Д |
Т |
П |
Ъ |
А |
Р |
В |
Й |
Г |
Г |
И |
Щ |
В |
Ч |
Э |
Е |
Ц |
С |
Т |
У |
Ж |
В |
С |
Е |
В |
|
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
|
В |
Н |
О |
Ч |
Ь |
Н |
А |
Д |
В |
А |
Д |
Ц |
А |
Т |
Ь |
В |
Т |
О |
Р |
О |
Е |
Я |
Н |
В |
А
|
|
Х |
А |
Х |
Я |
Ф |
Б |
Ь |
Б |
Е |
Т |
Ф |
З |
С |
Э |
Ф |
Т |
Х |
Ж |
З |
Б |
З |
Ъ |
Г |
Ф |
Б |
|
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
|
Р |
Я |
Т |
Ы |
С |
Я |
Ч |
А |
В |
О |
С |
Е |
М |
Ь |
С |
О |
Т |
Д |
В |
А |
Д |
Ц |
А |
Т |
Ь
|
|
Щ |
И |
Х |
Х |
Р |
И |
П |
Ж |
Т |
З |
В |
Т |
Ж |
Й |
Т |
Г |
О |
Й |
Б |
Н |
Т |
Ф |
Ф |
Е |
О |
|
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
|
Ш |
Е |
С |
Т |
О |
Г |
О |
Г |
О |
Д |
А |
Н |
Е |
Ж |
О |
А |
М |
Д |
А |
К |
О |
С |
Т |
А |
Н
|
|
И |
Х |
Т |
Т |
Е |
Г |
И |
И |
О |
К |
З |
П |
Т |
Ф |
Л |
Е |
У |
Г |
С |
Ф |
И |
П |
Т |
Ь |
М |
|
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
|
Е |
С |
П |
Р |
А |
В |
Е |
Д |
Л |
И |
В |
О |
П |
Р |
И |
Г |
О |
В |
О |
Р |
Е |
Н |
Н |
Ы |
Й
|
|
О |
Ф |
О |
К |
С |
Х |
М |
Г |
Б |
Т |
Ж |
Ф |
Ы |
Г |
У |
Ч |
О |
Ю |
Н |
Ф |
Н |
Ш |
З |
Г |
Э |
|
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
|
К |
С |
М |
Е |
Р |
Т |
И |
А |
Я |
Н |
Е |
С |
Ч |
А |
С |
Т |
Н |
Ы |
Й |
С |
Л |
У |
Ж |
А |
Щ
|
|
Л |
Л |
Ш |
Р |
У |
Д |
Е |
Н |
К |
О |
Л |
Г |
Г |
Н |
С |
Б |
К |
С |
С |
Е |
П |
У |
Н |
Ф |
Ц |
|
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
1 |
5 |
3 |
4 |
3 |
|
И |
Й |
У |
П |
Р |
А |
В |
Л |
Е |
Н |
И |
Я |
А |
Л |
М |
А |
З |
Н |
О |
Г |
О |
О |
К |
Р |
У
|
|
Е |
Е |
Е |
Г |
Г |
С |
Ж |
Н |
О |
Е |
Ы |
И |
О |
Н |
Р |
С |
И |
Т |
К |
Ц |
Ь |
Е |
Д |
Б |
У |
|
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
|
Г |
А |
Д |
А |
Я |
О |
Д |
И |
Н |
В |
Ч |
Е |
М |
И |
П |
О |
Д |
П |
И |
С |
Ы |
В |
А |
Ю |
С
|
|
Б |
Т |
Е |
Т |
Л |
О |
Т |
Б |
Ф |
Ц |
С |
Б |
Ю |
Й |
П |
М |
П |
З |
Т |
Ж |
П |
Т |
У |
Ф |
К |
|
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
1 |
3 |
4 |
3 |
2 |
5 |
|
Ь |
С |
В |
О |
И |
М |
Н |
А |
С |
Т |
О |
Я |
Щ |
И |
М |
И |
М |
Е |
Н |
Е |
М |
О |
Р |
Т |
Е
|
Итак, первая идея состоит в использовании вероятного слова,
то есть слова, которое с большой вероятностью может содержаться в
данном открытом тексте. Речь идет в том числе и о словах, часто
встречающихся в любых открытых текстах. К ним, например, относятся
такие слова как КОТОРЫЙ, ТОГДА, ЧТО, ЕСЛИ, приставки ПРИ, ПРЕ, ПОД и
т.п.
Вторая идея основана на том, что буквы открытого
сообщения находятся в открытом тексте на вполне определенных
позициях. Если разность номеров их позиций окажется кратной периоду
гаммы, то стоящие на этих позициях буквы будут
зашифрованы одним и тем
же знаком гаммы. Это означает, что определенные части открытого
текста окажутся зашифрованными шифром простой замены. Эту идею можно
использовать для определения периода ключа многоалфавитного шифра
замены.
Для определения периода гаммы могут быть применены два
способа. Первый из них известен как тест Казизки, второй способ
использует так называемый индекс совпадения.
Тест Казизки
был описан в 1863 году Фридрихом Казизки. Он
основан на следующем наблюдении: два одинаковых отрезка открытого
текста будут соответствовать двум одинаковым отрезкам шифрованного
текста, если разность номеров позиций их начал кратна периоду гаммы.
Следовательно, если мы обнаружим два одинаковых отрезка
шифрованного текста, состоящих по крайней мере из трех букв, то с
большой вероятностью им соответствуют одинаковые отрезки открытого
текста (случайное совпадение маловероятно). Тест Казизки, по сути,
заключается в том, что в шифрованном тексте надо найти пары
одинаковых отрезков, вычислить разности номеров позиций их начал
и определить общие делители найденных разностей. Как правило, один
из этих общих делителей равен периоду гаммы.
Для
уточнения значения периода гаммы может быть
использован индекс совпадения, предложенный в 1920 году Уильямом
Фридманом. Для последовательности букв индекс совпадения представляет
собой число, равное количеству всех пар номеров позиций
последовательности, на которых находятся одинаковые буквы, деленному на
общее количество всех пар номеров позиций этой последовательности,
т.е. среднему числу пар, состоящих из одинаковых букв.
Примечательно то, что при зашифровании последовательности с помощью
шифра простой замены указанное число не меняется.
Для иллюстрации этого подхода рассмотрим тот же самый
шифрованный текст, записанный в виде последовательности столбцов,
содержащих по шесть подряд идущих букв текста в каждом (подряд идущие
буквы текста располагаются в столбцах сверху вниз):
|
|
С |
Э |
Т |
Ф |
Р |
Ч |
Ж |
Д |
С |
А |
И |
Ц |
С |
Я |
Т |
Т |
Ъ |
Х |
Т |
Т |
Т |
Х |
И |
Ф |
Ф |
О |
М |
Ы |
Н |
Э |
Д |
Г |
С |
Ф |
Г |
Ы |
И |
Д |
Т |
Ц |
М |
Т |
|
Г |
Л |
Е |
Г |
Г |
Д |
Г |
Х |
Ю |
Р |
Щ |
С |
Е |
Ф |
Ф |
Х |
Г |
Х |
З |
Г |
Ф |
Т |
О |
Л |
И |
Ф |
Г |
Г |
Ф |
Л |
Е |
Г |
С |
Ц |
С |
И |
Т |
Б |
Л |
С |
П |
У |
|
У |
Л |
П |
И |
Й |
К |
У |
Р |
Д |
В |
В |
Т |
В |
Б |
З |
Ж |
Ф |
Р |
В |
О |
Ф |
Т |
К |
Е |
П |
О |
Б |
У |
Н |
Л |
Н |
Н |
Е |
Е |
Ж |
О |
К |
У |
О |
Б |
З |
Ф |
|
Ч |
З |
Н |
Н |
У |
О |
У |
Ъ |
Т |
Й |
Ч |
У |
Х |
Ь |
С |
З |
Б |
И |
Т |
Й |
Е |
Е |
З |
У |
Т |
К |
Т |
Ч |
Ш |
Ш |
К |
С |
У |
Е |
Н |
Н |
Ц |
Б |
Т |
Ю |
Т |
К |
|
П |
Й |
Л |
Б |
Г |
Т |
М |
С |
П |
Г |
Э |
Ж |
А |
Б |
Э |
Б |
Щ |
П |
Ж |
Б |
О |
Г |
П |
Г |
Ь |
С |
Ж |
О |
З |
Р |
О |
Б |
П |
Е |
О |
Р |
Ь |
Т |
Б |
Й |
Ж |
Д |
|
В |
Р |
Н |
О |
Л |
Х |
З |
Г |
Ъ |
Г |
Е |
В |
Х |
Е |
Ф |
З |
И |
Ж |
Й |
Н |
И |
И |
Т |
С |
М |
Х |
Ф |
Ю |
Г |
У |
Л |
К |
Н |
Г |
Е |
С |
Е |
Е |
Ф |
П |
П |
Г
|
|
Составим для каждой из 6 получившихся строк соответствующий ей
набор частот встречаемости букв в каждой из них:
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
Й |
К |
Л |
М |
Н |
О |
П |
|
1 строка |
1 |
0 |
0 |
2 |
3 |
0 |
1 |
0 |
3 |
0 |
0 |
0 |
2 |
1 |
1 |
0 |
|
2 строка |
0 |
1 |
0 |
9 |
1 |
3 |
0 |
1 |
2 |
0 |
0 |
4 |
0 |
0 |
1 |
1 |
|
3 строка |
0 |
3 |
4 |
0 |
1 |
3 |
2 |
2 |
1 |
1 |
3 |
2 |
0 |
3 |
4 |
2 |
|
4 строка |
0 |
2 |
0 |
0 |
0 |
4 |
0 |
3 |
1 |
2 |
3 |
0 |
0 |
4 |
1 |
0 |
|
5 строка |
1 |
6 |
0 |
4 |
1 |
1 |
4 |
1 |
0 |
2 |
0 |
0 |
1 |
0 |
4 |
5 |
|
6 строка |
0 |
0 |
2 |
5 |
0 |
5 |
1 |
2 |
3 |
1 |
1 |
2 |
1 |
3 |
1 |
2 |
|
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ъ |
Ы |
Ь |
Э |
Ю |
Я |
|
1 строка |
1 |
4 |
8 |
0 |
4 |
2 |
2 |
1 |
0 |
0 |
1 |
2 |
0 |
2 |
0 |
1 |
|
2 строка |
1 |
4 |
2 |
1 |
5 |
3 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
3 строка |
2 |
0 |
2 |
4 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
4 строка |
0 |
2 |
6 |
4 |
0 |
1 |
1 |
3 |
2 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
5 строка |
2 |
2 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
2 |
2 |
0 |
0 |
|
6 строка |
1 |
2 |
1 |
1 |
3 |
3 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
По этой таблице частот встречаемости букв вычислим для каждой строки
соответствующий ей индекс совпадения:
|
Номер строки |
1 |
2 |
3 |
4 |
5 |
6 |
|
Индекс совпадения |
0,060 |
0,077 |
0,045 |
0,053 |
0,057 |
0,057 |
|
Для всего шифрованного текста индекс совпадения равен 0,040,
что заметно меньше, чем индекс совпадения для каждой из указанных
строк. Это является хорошим подтверждением гипотезы о длине периода
гаммы.
Другие идеи подходов к вскрытию рассматриваемых шифров основаны на тех
или иных особенностях их построения и использования
(см. решения задач 1.2,
2.2,
2.5,
2.6,
3.4,
3.5,
4.6).
Next: 7.5. Условия задач олимпиад
Up: 7. Олимпиады по криптографии
Previous: Ответы к упражнению.
Contents: Содержание
|

