8. Подобные системы

Две секретные системы и будем называть подобными, если существует отображение , имеющее обратное , такое, что

Криптографический смысл подобия состоит в том, что если , то и  -- эквивалентны с точки зрения дешифрирования. Действительно, если шифровальщик противника перехватывает криптограмму из системы , он может перевести ее в криптограмму из системы простым применением к ней отображения . Обратно, криптограмма из системы переводится в криптограмму из системы с помощью . Если и применяются к одному и тому же пространству сообщений или языку, то имеется взаимооднозначное соответствие между получающимися криптограммами. Соответствующие друг другу криптограммы дают одинаковое апостериорное распределение вероятностей для всех сообщений.

Если имеется некоторый способ раскрытия системы , то любая система , подобная , может быть раскрыта после приведения ее к с помощью операции . Этот способ часто используется на практике.

В качестве тривиального примера рассмотрим простую подстановку, в которой буквы сообщения заменяются не буквами, а произвольными символами. Она подобна обычной простой подстановке с заменой на буквы. Вторым примером могут служить шифр Цезаря и обратный шифр Цезаря. Последний иногда раскрывают, переводя его сначала в шифр Цезаря. Это можно сделать, обратив алфавит в криптограмме. Шифры Виженера, Бофора и вариант Бофора все подобны, если ключ является случайным. Шифр с ``автоключом'' (т.е. сообщением, используемым в качестве ``ключа'') с используемыми вначале ключами подобен шифру Виженера с ключом, поочередно складываемым и вычитаемым по модулю 26. Отображение в этом случае представляет собой ``дешифровку'' автоключа с помощью последовательности из 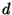таких отображений для каждого из начальных ключей.