Next: 2.5. Доказательства с нулевым
Up: 2. Криптография и теория
Previous: 2.3. Односторонние функции
Contents: Содержание
Существенный недостаток
шифра Вернама состоит в том, что
ключи одноразовые. Можно ли избавиться от этого недостатка
за счет некоторого снижения стойкости? Один из способов
решения этой проблемы состоит в следующем. Отправитель и
получатель имеют общий секретный ключ 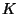 длины длины  и с
помощью некоторого достаточно эффективного алгоритма и с
помощью некоторого достаточно эффективного алгоритма  генерируют из него последовательность
генерируют из него последовательность  длины длины
 , где , где 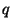 - некоторый полином. Такая криптосистема
(обозначим ее - некоторый полином. Такая криптосистема
(обозначим ее  ) позволяет шифровать сообщение ) позволяет шифровать сообщение  (или
совокупность сообщений) длиной до (или
совокупность сообщений) длиной до  битов по формуле битов по формуле
 , где , где  - поразрядное сложение
битовых строк по модулю 2. Дешифрование
выполняется по формуле - поразрядное сложение
битовых строк по модулю 2. Дешифрование
выполняется по формуле  . Из результатов Шеннона вытекает,
что такая
криптосистема не является абсолютно стойкой, т.е. стойкой
против любого противника (в чем, впрочем, нетрудно
убедиться и непосредственно). Но что будет, если требуется
защищаться только от полиномиально ограниченного
противника, который может атаковать криптосистему лишь с
помощью полиномиальных вероятностных алгоритмов? Каким
условиям должны удовлетворять последовательность . Из результатов Шеннона вытекает,
что такая
криптосистема не является абсолютно стойкой, т.е. стойкой
против любого противника (в чем, впрочем, нетрудно
убедиться и непосредственно). Но что будет, если требуется
защищаться только от полиномиально ограниченного
противника, который может атаковать криптосистему лишь с
помощью полиномиальных вероятностных алгоритмов? Каким
условиям должны удовлетворять последовательность  и
алгоритм и
алгоритм  , чтобы криптосистема , чтобы криптосистема  была стойкой? Поиски
ответов на эти вопросы привели к появлению понятия
псевдослучайного генератора, которое было введено Блюмом и
Микали [3]. была стойкой? Поиски
ответов на эти вопросы привели к появлению понятия
псевдослучайного генератора, которое было введено Блюмом и
Микали [3].
Пусть
 - функция,
вычислимая за полиномиальное (от - функция,
вычислимая за полиномиальное (от  ) время. Такая функция
называется генератором.
Интуитивно,
генератор ) время. Такая функция
называется генератором.
Интуитивно,
генератор  является
псевдослучайным, если порождаемые им последовательности
неотличимы никаким полиномиальным вероятностным
алгоритмом от случайных последовательностей той же
длины является
псевдослучайным, если порождаемые им последовательности
неотличимы никаким полиномиальным вероятностным
алгоритмом от случайных последовательностей той же
длины  . Формально этот объект определяется следующим
образом. . Формально этот объект определяется следующим
образом.
Пусть  - полиномиальная вероятностная машина Тьюринга,
которая получает на входе двоичные строки длины - полиномиальная вероятностная машина Тьюринга,
которая получает на входе двоичные строки длины  и
выдает в результате своей работы один бит. Пусть и
выдает в результате своей работы один бит. Пусть

Вероятность здесь определяется случайным выбором строки  и случайными величинами, которые
и случайными величинами, которые  использует в своей работе. Пусть
использует в своей работе. Пусть

Эта вероятность определяется случайным выбором
строки  и случайными величинами, которые и случайными величинами, которые  использует
в своей работе. Подчеркнем, что функция использует
в своей работе. Подчеркнем, что функция  вычисляется детерминированным алгоритмом.
вычисляется детерминированным алгоритмом.
Определение 2. Генератор  называется криптографически
стойким псевдослучайным генератором, если для любой
полиномиальной вероятностной машины Тьюринга называется криптографически
стойким псевдослучайным генератором, если для любой
полиномиальной вероятностной машины Тьюринга  , для любого
полинома , для любого
полинома 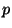 и всех достаточно больших и всех достаточно больших 

Всюду ниже мы для краткости будем называть
криптографически стойкие псевдослучайные генераторы просто
псевдослучайными генераторами. Такое сокращение является
общепринятым в криптографической литературе.
Нетрудно убедиться, что для существования псевдослучайных
генераторов необходимо существование односторонних функций.
В самом деле, сама функция  должна быть односторонней.
Доказательство этого простого факта мы оставляем читателю в
качестве упражнения. Вопрос о том, является ли
существование односторонних функций одновременно и
достаточным условием, долгое время оставался открытым. В
1982 г. Яо [10] построил псевдослучайный генератор,
исходя из предположения о существовании односторонних перестановок, т.е. сохраняющих длину взаимнооднозначных
односторонних функций. За этим последовала серия работ, в
которых достаточное условие все более и более ослаблялось,
пока наконец в 1989-1990 гг. Импальяццо, Левин и Луби [8]
и Хостад [6] не получили следующий окончательный
результат. должна быть односторонней.
Доказательство этого простого факта мы оставляем читателю в
качестве упражнения. Вопрос о том, является ли
существование односторонних функций одновременно и
достаточным условием, долгое время оставался открытым. В
1982 г. Яо [10] построил псевдослучайный генератор,
исходя из предположения о существовании односторонних перестановок, т.е. сохраняющих длину взаимнооднозначных
односторонних функций. За этим последовала серия работ, в
которых достаточное условие все более и более ослаблялось,
пока наконец в 1989-1990 гг. Импальяццо, Левин и Луби [8]
и Хостад [6] не получили следующий окончательный
результат.
Теорема 1.
Псевдослучайные генераторы существуют тогда и
только тогда, когда существуют односторонние функции.
Псевдослучайные генераторы находят применение не только в
криптографии, но и в теории сложности, и в других областях
дискретной математики. Обсуждение этих приложений выходит
за рамки настоящей главы. Здесь же в качестве
иллюстрации мы рассмотрим описанную в начале данного
раздела криптосистему  , использующую псевдослучайный
генератор в качестве алгоритма , использующую псевдослучайный
генератор в качестве алгоритма  . Прежде всего, нам
необходимо дать определение стойкости криптосистемы с
секретным ключом. . Прежде всего, нам
необходимо дать определение стойкости криптосистемы с
секретным ключом.
Пусть 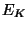 - алгоритм шифрования криптосистемы с
секретным ключом. Обозначим результат его работы - алгоритм шифрования криптосистемы с
секретным ключом. Обозначим результат его работы  ,
здесь ,
здесь 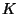 - секретный ключ длиной - секретный ключ длиной  битов, а
битов, а  - открытый текст длиной - открытый текст длиной  битов. Через битов. Через
 обозначается обозначается 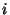 -ый бит открытого текста.
Пусть -ый бит открытого текста.
Пусть  - полиномиальная вероятностная машина Тьюринга, которая
получает на вход криптограмму - полиномиальная вероятностная машина Тьюринга, которая
получает на вход криптограмму 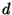 и выдает пару и выдает пару  , где , где
 , ,
 .
Интуитивно, криптосистема является стойкой, если никакая
машина Тьюринга .
Интуитивно, криптосистема является стойкой, если никакая
машина Тьюринга  не может вычислить ни один бит
открытого текста с вероятностью успеха, существенно
большей, чем при простом угадывании. не может вычислить ни один бит
открытого текста с вероятностью успеха, существенно
большей, чем при простом угадывании.
Определение 3. Криптосистема называется стойкой, если для
любой полиномиальной вероятностной машины Тьюринга  , для
любого полинома , для
любого полинома 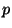 и всех достаточно больших и всех достаточно больших 

Эта вероятность (всюду ниже для краткости мы ее обозначаем
просто  ) определяется случайным выбором секретного
ключа ) определяется случайным выбором секретного
ключа 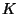 , случайным выбором открытого текста , случайным выбором открытого текста  из множества
всех двоичных строк длины из множества
всех двоичных строк длины  и случайными величинами, которые и случайными величинами, которые
 использует в своей работе. использует в своей работе.
Покажем, что криптосистема  с псевдослучайным
генератором в качестве с псевдослучайным
генератором в качестве  является стойкой в смысле
данного определения. Предположим противное, т.е. что
существуют полиномиальный вероятностный алгоритм является стойкой в смысле
данного определения. Предположим противное, т.е. что
существуют полиномиальный вероятностный алгоритм  и
полином и
полином 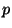 такие, что такие, что
 для бесконечно
многих для бесконечно
многих  . Рассмотрим алгоритм . Рассмотрим алгоритм  , который получает на
входе двоичную строку , который получает на
входе двоичную строку  длины длины  , выбирает , выбирает
 , вычисляет , вычисляет  и вызывает и вызывает  как подпрограмму, подавая ей на вход строку
как подпрограмму, подавая ей на вход строку 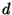 . Получив
от . Получив
от  пару пару  , ,  проверяет, действительно ли проверяет, действительно ли
 и если да, то выдает 1, в противном случае -
0, и останавливается. Легко видеть, что и если да, то выдает 1, в противном случае -
0, и останавливается. Легко видеть, что  работает за
полиномиальное (от работает за
полиномиальное (от  ) время. Убедимся, что алгоритм ) время. Убедимся, что алгоритм  отличает псевдослучайные строки, порожденные генератором
отличает псевдослучайные строки, порожденные генератором
 , от случайных строк длины , от случайных строк длины  . В самом деле, если
строки . В самом деле, если
строки  , поступающие на вход , поступающие на вход  , являются случайными,
то , являются случайными,
то 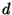 - криптограмма шифра Вернама и, согласно теореме
Шеннона, - криптограмма шифра Вернама и, согласно теореме
Шеннона,  . Если строки . Если строки  порождены генератором порождены генератором
 , то криптограммы , то криптограммы 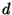 имеют такое же распределение
вероятностей, как в криптосистеме имеют такое же распределение
вероятностей, как в криптосистеме  , и, согласно
предположению, , и, согласно
предположению,
 для бесконечно многих для бесконечно многих  .
Полученное противоречие с определением
псевдослучайного генератора доказывает утверждение о
стойкости криптосистемы .
Полученное противоречие с определением
псевдослучайного генератора доказывает утверждение о
стойкости криптосистемы  . .
Разумеется, стойкость криптосистемы с секретным ключом
можно определять различным образом. Например, можно
рассматривать стойкость против атаки с выбором открытого
текста: противник может предварительно выбрать
полиномиальное количество открытых текстов и получить их
криптограммы, после чего он получает ту криптограмму, по
которой ему требуется вычислить хотя бы один бит
соответствующего открытого текста. Нетрудно убедиться, что
криптосистема  с псевдослучайным генератором в качестве с псевдослучайным генератором в качестве  является
стойкой и против атаки с выбором открытого текста. является
стойкой и против атаки с выбором открытого текста.
Таким образом, мы убедились, что с помощью псевдослучайных
генераторов можно строить стойкие криптосистемы. Основное
направление исследований в данной области - поиск методов
построения эффективных псевдослучайных генераторов на
основе различных криптографических предположений.
Показателем эффективности здесь служит количество
операций, затрачиваемых на вычисление каждого очередного
бита псевдослучайной последовательности.
Next: 2.5. Доказательства с нулевым
Up: 2. Криптография и теория
Previous: 2.3. Односторонние функции
Contents: Содержание
|

