Next: Литература к главе 2
Up: 2. Криптография и теория
Previous: 2.4. Псевдослучайные генераторы
Contents: Содержание
Предположим, что Алиса знает доказательство некоторой
теоремы и желает убедить Боба в том, что теорема верна.
Конечно, Алиса может просто передать доказательство Бобу на
проверку. Но тогда впоследствии Боб сможет сам, без помощи
Алисы, доказывать третьим лицам эту теорему. А может ли
Алиса убедить Боба так, чтобы он не получил при этом
никакой информации, которая помогла бы ему восстановить
доказательство теоремы? Этим двум, казалось бы
взаимно исключающим требованиям, удовлетворяют протоколы
доказательства с нулевым разглашением. Последнее понятие
было введено Гольдвассер, Микали и Ракоффом в 1985 г.
[4].
Рассматривается следующая модель протокола. В распоряжении
Алисы и Боба имеются вероятностные машины Тьюринга P
и V
соответственно. Вычислительные ресурсы, которые может
использовать Алиса, неограничены, в то время как машина V
работает за полиномиальное время. Машины P и V имеют
общую коммуникационную ленту для обмена сообщениями. После
записи сообщения на коммуникационную ленту машина переходит
в состояние ожидания и выходит из него, как только на ленту
будет записано ответное сообщение. Машины P и V имеют
также общую входную ленту, на которую записано входное
слово 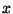 . Утверждение, которое доказывает Алиса, суть
`` . Утверждение, которое доказывает Алиса, суть
`` '', где '', где 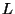 - некоторый фиксированный (известный
и Алисе, и Бобу) язык. Чтобы избежать тривиальности, язык - некоторый фиксированный (известный
и Алисе, и Бобу) язык. Чтобы избежать тривиальности, язык
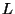 должен быть трудным (например, NP-полным), иначе Боб
сможет самостоятельно проверить, что должен быть трудным (например, NP-полным), иначе Боб
сможет самостоятельно проверить, что  . По существу,
протокол доказательства состоит в том, что Боб, используя
случайность, выбирает некоторые вопросы, задает их Алисе и
проверяет правильность ответов. Выполнение протокола
завершается, когда машина V останавливается, при этом она
выдает 1, если
доказательство принято, и 0 - в противном
случае. . По существу,
протокол доказательства состоит в том, что Боб, используя
случайность, выбирает некоторые вопросы, задает их Алисе и
проверяет правильность ответов. Выполнение протокола
завершается, когда машина V останавливается, при этом она
выдает 1, если
доказательство принято, и 0 - в противном
случае.
Пусть  и и  - две интерактивные,
т.е. взаимодействующие через общую коммуникационную ленту, вероятностные
машины Тьюринга. Через - две интерактивные,
т.е. взаимодействующие через общую коммуникационную ленту, вероятностные
машины Тьюринга. Через ![$ [B(x),A(x)]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img141.gif) обозначается
случайная величина - выходное слово машины обозначается
случайная величина - выходное слово машины  ,
когда ,
когда  и и  работают на входном слове работают на входном слове 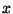 .
Через .
Через  обозначается длина слова обозначается длина слова 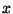 . .
Определение 4. Интерактивным доказательством для языка 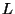 называется пара интерактивных машин Тьюринга
называется пара интерактивных машин Тьюринга
 такая,
что выполняются следующие два условия. такая,
что выполняются следующие два условия.
1. (Полнота). Для всех 
![\begin{displaymath}Pr\{ [\mathbf P(x),\mathbf V(x)]=1\} =1.\end{displaymath}](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img144.gif)
2. (Корректность). Для любой машины Тьюринга  , для
любого полинома , для
любого полинома 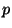 и для всех и для всех  достаточно
большой длины достаточно
большой длины
![\begin{displaymath}Pr\{ [\mathbf P^*(x),\mathbf V(x)]=1\} < 1/p(\vert x\vert).\end{displaymath}](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img146.gif)
Полнота означает, что если входное слово принадлежит языку
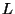 и оба участника, и Алиса, и Боб, следуют протоколу, то
доказательство будет всегда принято. Требование
корректности защищает Боба от нечестной Алисы, которая
пытается обмануть его, ``доказывая'' ложное
утверждение. При этом Алиса может каким угодно образом
отклоняться от действий, предписанных протоколом, т.е. вместо машины Тьюринга P использовать любую другую
машину и оба участника, и Алиса, и Боб, следуют протоколу, то
доказательство будет всегда принято. Требование
корректности защищает Боба от нечестной Алисы, которая
пытается обмануть его, ``доказывая'' ложное
утверждение. При этом Алиса может каким угодно образом
отклоняться от действий, предписанных протоколом, т.е. вместо машины Тьюринга P использовать любую другую
машину  . Требуется, чтобы вероятность обмана была в
любом случае пренебрежимо малой. . Требуется, чтобы вероятность обмана была в
любом случае пренебрежимо малой.
Определение 5. Интерактивный протокол доказательства для
языка 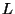 называется доказательством с абсолютно нулевым
разглашением, если, кроме условий 1 и 2, выполнено еще и следующее
условие. называется доказательством с абсолютно нулевым
разглашением, если, кроме условий 1 и 2, выполнено еще и следующее
условие.
3. (Свойство нулевого разглашения). Для любой
полиномиальной вероятностной машины Тьюринга  существует вероятностная машина Тьюринга
существует вероятностная машина Тьюринга
 ,
работающая за полиномиальное в среднем время, и такая, что
для всех ,
работающая за полиномиальное в среднем время, и такая, что
для всех 
![\begin{displaymath}\mathbf M_{\mathbf V^*}(x)=[\mathbf P(x),\mathbf V^*(x)].\end{displaymath}](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img149.gif)
Машина
 называется моделирующей машиной для
называется моделирующей машиной для  .
Предполагается, что математическое ожидание времени ее
работы ограничено полиномом от длины .
Предполагается, что математическое ожидание времени ее
работы ограничено полиномом от длины 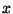 .
Это означает, что
в принципе .
Это означает, что
в принципе
 может, в зависимости от того, какие
значения примут используемые в ее работе случайные
переменные, работать достаточно долго. Но вероятность того,
что время ее работы превысит некоторую полиномиальную
границу, мала. Для каждой машины может, в зависимости от того, какие
значения примут используемые в ее работе случайные
переменные, работать достаточно долго. Но вероятность того,
что время ее работы превысит некоторую полиномиальную
границу, мала. Для каждой машины  строится своя
моделирующая машина; последняя может использовать строится своя
моделирующая машина; последняя может использовать  как
подпрограмму. Через как
подпрограмму. Через
 обозначается
случайная величина - выходное слово машины обозначается
случайная величина - выходное слово машины
 , когда на входе она получает слово , когда на входе она получает слово 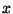 . .
Свойство нулевого разглашения защищает Алису от нечестного
Боба, который, произвольно отклоняясь от действий,
предписанных протоколом (используя  вместо V),
пытается извлечь из его выполнения дополнительную
информацию. Условие 3 означает, что Боб может при этом
получить только такую информацию, которую
он смог бы вычислить и самостоятельно (без выполнения
протокола) за полиномиальное время. вместо V),
пытается извлечь из его выполнения дополнительную
информацию. Условие 3 означает, что Боб может при этом
получить только такую информацию, которую
он смог бы вычислить и самостоятельно (без выполнения
протокола) за полиномиальное время.
Приведем в качестве примера протокол доказательства с
абсолютно нулевым разглашением для языка
ИЗОМОРФИЗМ ГРАФОВ из работы Гольдрайха, Микали и
Вигдерсона [5].
Входным словом является пара графов  и и
 . Здесь . Здесь 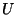 - множество вершин, которое
можно отождествить с множеством натуральных чисел - множество вершин, которое
можно отождествить с множеством натуральных чисел
 , ,  и и  - множества ребер такие, что - множества ребер такие, что
 . Графы . Графы  и и  называются
изоморфными, если существует перестановка называются
изоморфными, если существует перестановка  на
множестве на
множестве 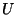 такая, что такая, что  тогда и только
тогда, когда тогда и только
тогда, когда
 (обозначается
(обозначается
 ). Задача распознавания
изоморфизма графов - хорошо известная математическая
задача, для которой на данный момент не известно
полиномиальных алгоритмов. С другой стороны, неизвестно,
является ли эта задача NP-полной, хотя есть веские
основания предполагать, что не является. ). Задача распознавания
изоморфизма графов - хорошо известная математическая
задача, для которой на данный момент не известно
полиномиальных алгоритмов. С другой стороны, неизвестно,
является ли эта задача NP-полной, хотя есть веские
основания предполагать, что не является.
Протокол IG
Пусть  - изоморфизм между - изоморфизм между  и и  .
Следующие четыре шага выполняются в цикле .
Следующие четыре шага выполняются в цикле
 раз, каждый раз с независимыми случайными величинами. раз, каждый раз с независимыми случайными величинами.
P выбирает случайную перестановку  на множестве на множестве
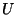 , вычисляет , вычисляет  и посылает этот граф V. и посылает этот граф V.
V выбирает случайный бит  и посылает его P. и посылает его P.
Если  , то P посылает V перестановку , то P посылает V перестановку  ,
в противном случае - перестановку ,
в противном случае - перестановку
 . .
Если перестановка, полученная V, не является
изоморфизмом
между  и и 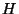 , то V останавливается
и отвергает доказательство. В противном случае выполнение
протокола продолжается. , то V останавливается
и отвергает доказательство. В противном случае выполнение
протокола продолжается.
Если проверки п.4 дали положительный результат во всех  циклах, то V принимает доказательство.
циклах, то V принимает доказательство.
Заметим, что если в протоколе IG машина P получает
изоморфизм  в качестве дополнительного входного
слова, то ей для выполнения протокола не требуются
неограниченные вычислительные ресурсы. Более того, в этом
случае P может быть полиномиальной вероятностной
машиной Тьюринга. в качестве дополнительного входного
слова, то ей для выполнения протокола не требуются
неограниченные вычислительные ресурсы. Более того, в этом
случае P может быть полиномиальной вероятностной
машиной Тьюринга.
Теорема 2. ([5])
Протокол IG является доказательством с
абсолютно нулевым разглашением для языка ИЗОМОРФИЗМ ГРАФОВ.
Полнота протокола IG очевидна.
Для доказательства
корректности достаточно заметить, что бит  , который
V выбирает на шаге 2, указывает P, для какого из графов
- , который
V выбирает на шаге 2, указывает P, для какого из графов
-  или или  - требуется продемонстрировать
изоморфизм с графом - требуется продемонстрировать
изоморфизм с графом 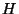 . Если . Если  и и  не изоморфны,
то не изоморфны,
то 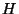 может быть изоморфен, в лучшем случае, одному из них.
Поэтому проверка п. 4 даст положительный результат с
вероятностью может быть изоморфен, в лучшем случае, одному из них.
Поэтому проверка п. 4 даст положительный результат с
вероятностью  в одном цикле и с вероятностью в одном цикле и с вероятностью
 во всех во всех  циклах. циклах.
Доказательство свойства нулевого разглашения значительно
сложнее. Поэтому мы воспроизводим только основную идею.
Прежде всего, заметим, что основная задача машины  -
получить максимально возможную информацию об изоморфизме
между -
получить максимально возможную информацию об изоморфизме
между  и и  . Естественно предположить, что она,
в отличие от V, будет выдавать в качестве выходного слова
не один бит, а всю полученную в результате выполнения
протокола информацию, включая
содержимое своей случайной ленты,
графы . Естественно предположить, что она,
в отличие от V, будет выдавать в качестве выходного слова
не один бит, а всю полученную в результате выполнения
протокола информацию, включая
содержимое своей случайной ленты,
графы 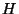 и перестановки,
полученные соответственно на шагах 1 и 3 протокола IG.
Моделирующая машина и перестановки,
полученные соответственно на шагах 1 и 3 протокола IG.
Моделирующая машина
 должна уметь строить
такие же случайные строки, графы
и перестановки, не зная при этом изоморфизм должна уметь строить
такие же случайные строки, графы
и перестановки, не зная при этом изоморфизм  ! Поэтому ! Поэтому
 пытается угадать тот бит пытается угадать тот бит  , который будет запросом
машины , который будет запросом
машины  на шаге 2. Для этого на шаге 2. Для этого
 выбирает
случайный бит выбирает
случайный бит  , случайную перестановку , случайную перестановку  и вычисляет и вычисляет
 . Далее . Далее
 запоминает состояние машины запоминает состояние машины
 (включая содержимое случайной ленты)
и вызывает ее как подпрограмму, подавая ей на вход граф (включая содержимое случайной ленты)
и вызывает ее как подпрограмму, подавая ей на вход граф 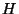 . Ответом машины . Ответом машины
 будет некоторый бит будет некоторый бит  . Если . Если  ,
то моделирование в данном цикле завершено успешно,
поскольку ,
то моделирование в данном цикле завершено успешно,
поскольку
 может продемонстрировать требуемый
изоморфизм. Если же может продемонстрировать требуемый
изоморфизм. Если же
 , то , то
 восстанавливает ранее сохраненное состояние машины
восстанавливает ранее сохраненное состояние машины  и
повторяет попытку. и
повторяет попытку.
Если
в определении свойства нулевого разглашения заменить
равенство случайных величин
 и и
![$ [\mathbf P(x),\mathbf V^*(x)]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img177.gif) требованием, чтобы их
распределения вероятностей ``почти не отличались'', то
получится другая разновидность доказательств -
доказательства со статистически нулевым разглашением. требованием, чтобы их
распределения вероятностей ``почти не отличались'', то
получится другая разновидность доказательств -
доказательства со статистически нулевым разглашением.
Еще один тип - доказательства с вычислительно нулевым
разглашением. В этом случае требуется, чтобы моделирующая
машина создавала распределение вероятностей, которое
неотличимо от
![$ [\mathbf P(x),\mathbf V^*(x)]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img177.gif) никаким
полиномиальным вероятностным алгоритмом (неотличимость
здесь определяется аналогично тому, как это делалось в
определении псевдослучайного генератора). никаким
полиномиальным вероятностным алгоритмом (неотличимость
здесь определяется аналогично тому, как это делалось в
определении псевдослучайного генератора).
Подчеркнем особо,
что во всех трех определениях нулевого разглашения условия
накладываются на действия моделирующей машины только на тех
словах, которые принадлежат языку.
Помимо интереса к доказательствам с нулевым разглашением
как к нетривиальному математическому объекту, они
исследуются также и в связи с практическими приложениями.
Наиболее естественный и важный тип таких
приложений - протоколы аутентификации
(см. главу 3). С помощью такого
протокола Алиса может доказать
Бобу свою аутентичность.
Предположим, например, что Алиса - это
интеллектуальная банковская карточка, в которой реализован алгоритм
P, а Боб - это компьютер банка, выполняющий программу V.
Прежде чем начать выполнение каких-либо банковских операций, банк
должен убедиться в подлинности карточки и идентифицировать ее
владельца, или, говоря на языке криптографии, карточка
должна пройти аутентификацию. В принципе для этой цели
можно использовать приведенный выше протокол IG. В этом
случае в памяти банковского компьютера хранится пара
графов  , сопоставленная Алисе, а на
интеллектуальной карточке - та же пара графов и
изоморфизм , сопоставленная Алисе, а на
интеллектуальной карточке - та же пара графов и
изоморфизм  . Предполагается, что, кроме Алисы, этот
изоморфизм никто не знает (кроме, быть может, Боба) и
поэтому с помощью протокола IG карточка доказывает свою
аутентичность. При
этом свойство полноты означает, что карточка наверняка
докажет свою аутентичность. Свойство корректности защищает
интересы банка от злоумышленника, который, не являясь
клиентом банка, пытается пройти аутентификацию, используя
фальшивую карточку. Свойство нулевого разглашения защищает
клиента от злоумышленника, который, подслушав одно или более
выполнений протокола аутентификации данной
карточки, пытается пройти аутентификацию под именем
Алисы.
Конечно, в данном случае бессмысленно доказывать, что пара графов . Предполагается, что, кроме Алисы, этот
изоморфизм никто не знает (кроме, быть может, Боба) и
поэтому с помощью протокола IG карточка доказывает свою
аутентичность. При
этом свойство полноты означает, что карточка наверняка
докажет свою аутентичность. Свойство корректности защищает
интересы банка от злоумышленника, который, не являясь
клиентом банка, пытается пройти аутентификацию, используя
фальшивую карточку. Свойство нулевого разглашения защищает
клиента от злоумышленника, который, подслушав одно или более
выполнений протокола аутентификации данной
карточки, пытается пройти аутентификацию под именем
Алисы.
Конечно, в данном случае бессмысленно доказывать, что пара графов
 принадлежит языку ИЗОМОРФИЗМ ГРАФОВ, поскольку она
заведомо выбирается из этого языка. Вместо этого Алиса доказывает, что
она знает изоморфизм принадлежит языку ИЗОМОРФИЗМ ГРАФОВ, поскольку она
заведомо выбирается из этого языка. Вместо этого Алиса доказывает, что
она знает изоморфизм  . Интерактивные
доказательства такого типа называются доказательствами знания. . Интерактивные
доказательства такого типа называются доказательствами знания.
Для практического применения очень важным свойством
протокола IG, как и других протоколов доказательства знания,
является то, что алгоритм P, получивший
в качестве дополнительного входа изоморфизм  ,
работает за полиномиальное время. Вместо протокола IG
можно использовать, вообще говоря, любое другое
доказательство с нулевым разглашением, в котором алгоритм
P обладает этим свойством. Но для
реальных приложений протокол IG, как и большинство
подобных протоколов, не эффективен: большое
количество циклов, слишком длинные сообщения и т.д.
Поиск более эффективных доказуемо стойких протоколов -
одно из основных направлений исследований в данной области. ,
работает за полиномиальное время. Вместо протокола IG
можно использовать, вообще говоря, любое другое
доказательство с нулевым разглашением, в котором алгоритм
P обладает этим свойством. Но для
реальных приложений протокол IG, как и большинство
подобных протоколов, не эффективен: большое
количество циклов, слишком длинные сообщения и т.д.
Поиск более эффективных доказуемо стойких протоколов -
одно из основных направлений исследований в данной области.
Next: Литература к главе 2
Up: 2. Криптография и теория
Previous: 2.4. Псевдослучайные генераторы
Contents: Содержание
|

