Next: ...к задачам третьей олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам первой олимпиады
Contents: Содержание
2.1. Рассмотрим один виток ленты на развертке цилиндра (разрез
по горизонтальной линии). По условию высота  , опущенная на
сторону , опущенная на
сторону  , равна , равна 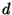 . Угол . Угол  равен равен
 .
Отсюда .
Отсюда 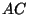 равно равно  . Так как высота строки равна . Так как высота строки равна  ,
то всего на одном витке ,
то всего на одном витке
 букв. букв.
Ответ: чтобы прочитать текст, надо разрезать ленту на
участки по
 букв и сложить их рядом. букв и сложить их рядом.
2.2. Согласно условию, исходное сообщение состоит из двух
пятерок цифр:
 и и
 .
Пусть .
Пусть  - последние две цифры суммы чисел,
изображенных этими пятерками. Через - последние две цифры суммы чисел,
изображенных этими пятерками. Через  обозначим последнюю цифру
суммы чисел обозначим последнюю цифру
суммы чисел  и и  . Пусть . Пусть 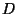 обозначает цифру переноса (цифру
десятков) суммы обозначает цифру переноса (цифру
десятков) суммы  . По условию имеем, что . По условию имеем, что
 и и
 . .
Пусть  - первый член, а - первый член, а  - разность
арифметической прогрессии, которую коммерсант использовал при
шифровании. Тогда из условия получаем: - разность
арифметической прогрессии, которую коммерсант использовал при
шифровании. Тогда из условия получаем:

Обозначим символом  равенство остатков от деления на 10
чисел равенство остатков от деления на 10
чисел  и и  . Тогда записи . Тогда записи  и и  имеют одинаковый смысл. Если
имеют одинаковый смысл. Если  и и  , то , то
 , ,  . Bсегда . Bсегда  , так как остаток
от деления единствен. , так как остаток
от деления единствен.
Из соотношений (4), (5), (9) и (10)
находим соответственно:

Подставляя эти значения в равенства
(11) и (12), получим следующие
равенства:
 и и
 .
Отсюда следует, что .
Отсюда следует, что

Подставив  из (17) и из (17) и  из (18) в (1),
(2),(3), (13), (14), (6), (7),
(8), (15), (16), найдем выражения для цифр исходного
сообщения: из (18) в (1),
(2),(3), (13), (14), (6), (7),
(8), (15), (16), найдем выражения для цифр исходного
сообщения:

Найденные выражения дают два варианта исходных
сообщений:
|
4470416411 (при  ), 2371640978 (при ), 2371640978 (при  ). ). |
2.3. Ответ:  - любое, - любое,  - не должно делиться на 2 и на 5. - не должно делиться на 2 и на 5.
Указание. Обозначим через 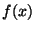 - остаток от деления значения
многочлена - остаток от деления значения
многочлена  на 10. Для однозначного расшифрования необходимо
и достаточно, чтобы разным значениям на 10. Для однозначного расшифрования необходимо
и достаточно, чтобы разным значениям 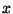 соответствовали разные
значения соответствовали разные
значения 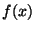 . Поэтому . Поэтому  , ,  , ..., , ...,  принимают все значения от 0 до 9. Найдем эти значения:
принимают все значения от 0 до 9. Найдем эти значения:

где  - остаток от деления числа - остаток от деления числа 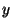 на 10. на 10.
Отсюда, пользуясь свойствами остатков, замечаем, что  должно
быть нечетным (иначе должно
быть нечетным (иначе 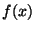 будут только четные числа) и будут только четные числа) и  не
должно делиться на 5 (иначе не
должно делиться на 5 (иначе 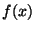 будут только 0 и 5).
Непосредственной проверкой можно убедиться, что
при любом будут только 0 и 5).
Непосредственной проверкой можно убедиться, что
при любом  и при всех и при всех  ,
удовлетворяющим приведенным условиям, гарантируется
однозначность расшифрования. ,
удовлетворяющим приведенным условиям, гарантируется
однозначность расшифрования.
2.4. Обозначим через  остаток от деления на
26 суммы чисел, которые
соответствуют первым
остаток от деления на
26 суммы чисел, которые
соответствуют первым  буквам алфавита
( буквам алфавита
(
 ) )
 . .
Если среди чисел
 есть нуль: есть нуль:  ,
то искомой
ключевой комбинацией является цепочка первых ,
то искомой
ключевой комбинацией является цепочка первых  букв алфавита. букв алфавита.
Если среди чисел
 нет нуля, то обязательно найдутся два
одинаковых числа: нет нуля, то обязательно найдутся два
одинаковых числа:  (считаем, что (считаем, что  ). Тогда искомой ключевой
комбинацией является участок алфавита, начинающийся с ). Тогда искомой ключевой
комбинацией является участок алфавита, начинающийся с
 -й и заканчивающийся -й и заканчивающийся  -й буквой. -й буквой.
2.5.
Если две буквы с порядковыми номерами  и и  зашифрованы в буквы с
порядковыми номерами
зашифрованы в буквы с
порядковыми номерами  и и  с помощью одной и той же буквы, то остатки от
деления чисел
с помощью одной и той же буквы, то остатки от
деления чисел  и и  на 30
равны между собой и совпадают с
порядковым номером шифрующей буквы (порядковым номером буквы на 30
равны между собой и совпадают с
порядковым номером шифрующей буквы (порядковым номером буквы  удобно
считать число 0). Тогда, с учетом соглашения о порядковом номере буквы удобно
считать число 0). Тогда, с учетом соглашения о порядковом номере буквы  ,
справедливо, что ,
справедливо, что  равен остатку от деления числа равен остатку от деления числа
 на 30, а, вместе с
тем, на 30, а, вместе с
тем,  равен остатку от деления числа равен остатку от деления числа
 на 30. Если каждое из
выражений в скобках заменить соответствующим остатком от деления на 30, то
упомянутая связь не нарушится. на 30. Если каждое из
выражений в скобках заменить соответствующим остатком от деления на 30, то
упомянутая связь не нарушится.
Представим в виде набора порядковых номеров известные шифрованные
сообщения (обозначим их соответственно ш. с. 1 и ш. с. 2) и
слово КОРАБЛИ:
|
слово |
К |
О |
Р |
А |
Б |
Л |
И |
 |
10 |
14 |
16 |
1 |
2 |
11 |
9 |
|
ш.с.1 |
Ю |
П |
Т |
Ц |
А |
Р |
Г |
Ш |
А |
Л |
Ж |
Ж |
Е |
В |
Ц |
Щ |
Ы |
Р |
В |
У |
У |
 |
29 |
15 |
18 |
22 |
1 |
16 |
4 |
24 |
1 |
11 |
7 |
7 |
6 |
3 |
22 |
25 |
27 |
16 |
3 |
19 |
19 |
|
ш.с.2 |
Ю |
П |
Я |
Т |
Б |
Н |
Щ |
М |
С |
Д |
Т |
Л |
Ж |
Г |
П |
С |
Г |
Х |
С |
Ц |
Ц |
 |
29 |
15 |
0 |
18 |
2 |
13 |
25 |
12 |
17 |
5 |
18 |
11 |
7 |
4 |
15 |
17 |
4 |
21 |
17 |
22 |
22 |
Возможны 15 вариантов
(номер варианта обозначим буквой  )
расположения слова
КОРАБЛИ
в каждом из двух исходных сообщений (и. с. 1, и. с. 2). )
расположения слова
КОРАБЛИ
в каждом из двух исходных сообщений (и. с. 1, и. с. 2).
Вначале для каждого из 15 вариантов расположения слова
КОРАБЛИ
в и. с. 1 найдем соответствующий участок и. с. 2.
Имеем:
 |
0 |
0 |
12 |
26 |
1 |
27 |
21 |
18 |
16 |
24 |
11 |
4 |
1 |
1 |
23 |
22 |
7 |
5 |
14 |
3 |
3 |
Поэтому для участка и. с. 2 получаем
следующие 15 вариантов:
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
 |
10 |
10 |
22 |
6 |
11 |
7 |
1 |
28 |
26 |
4 |
21 |
14 |
11 |
11 |
3 |
 |
14 |
26 |
10 |
15 |
11 |
5 |
2 |
0 |
8 |
25 |
18 |
15 |
15 |
7 |
6 |
 |
28 |
12 |
17 |
13 |
7 |
4 |
2 |
10 |
27 |
20 |
17 |
17 |
9 |
8 |
23 |
 |
27 |
2 |
28 |
22 |
19 |
17 |
25 |
12 |
5 |
2 |
2 |
24 |
23 |
8 |
6 |
 |
3 |
29 |
23 |
20 |
18 |
26 |
13 |
6 |
3 |
3 |
25 |
24 |
9 |
7 |
16 |
 |
28 |
2 |
29 |
27 |
5 |
22 |
15 |
12 |
12 |
4 |
3 |
18 |
16 |
25 |
14 |
 |
0 |
27 |
25 |
3 |
20 |
13 |
10 |
10 |
2 |
1 |
16 |
14 |
23 |
12 |
12 |
Теперь для каждого из 15 вариантов расположения слова
КОРАБЛИ
в и. с. 2 найдем соответствующий участок и. с. 1.
Имеем:
 |
0 |
0 |
18 |
4 |
29 |
3 |
9 |
12 |
14 |
6 |
19 |
26 |
29 |
29 |
7 |
8 |
23 |
25 |
16 |
27 |
27 |
Поэтому для участка и. с. 1 получаем
следующие 15 вариантов:
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
 |
10 |
10 |
28 |
14 |
9 |
13 |
19 |
22 |
24 |
16 |
29 |
6 |
9 |
9 |
17 |
 |
14 |
2 |
18 |
13 |
17 |
23 |
26 |
28 |
20 |
3 |
10 |
13 |
13 |
21 |
22 |
 |
4 |
20 |
15 |
19 |
25 |
28 |
0 |
22 |
5 |
12 |
15 |
15 |
23 |
24 |
9 |
 |
5 |
0 |
4 |
10 |
13 |
15 |
7 |
20 |
27 |
0 |
0 |
8 |
9 |
24 |
26 |
 |
1 |
5 |
11 |
14 |
16 |
8 |
21 |
28 |
1 |
1 |
9 |
10 |
25 |
27 |
18 |
 |
14 |
20 |
23 |
25 |
17 |
0 |
7 |
10 |
10 |
18 |
19 |
4 |
6 |
27 |
8 |
 |
18 |
21 |
23 |
15 |
28 |
5 |
8 |
8 |
16 |
17 |
2 |
4 |
25 |
6 |
6 |
Заменим порядковые номера
в найденных вариантах участков и. с. 1 и и. с. 2
на буквы русского алфавита. Получаем следующие
таблицы:
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
К |
К |
Ц |
Е |
Л |
Ж |
А |
Э |
Ь |
Г |
Х |
О |
Л |
Л |
В |
|
О |
Ь |
К |
П |
Л |
Д |
Б |
Я |
З |
Щ |
Т |
П |
П |
Ж |
Е |
|
участок |
Э |
М |
С |
Н |
Ж |
Г |
Б |
К |
Ы |
Ф |
С |
С |
И |
З |
Ч |
|
и.с.2 |
Ы |
Б |
Э |
Ц |
У |
С |
Щ |
М |
Д |
Б |
Б |
Ш |
Ч |
З |
Е |
|
В |
Ю |
Ч |
Ф |
Т |
Ь |
Н |
Е |
В |
В |
Щ |
Ш |
И |
Ж |
Р |
|
Э |
Б |
Ю |
Ы |
Д |
Ц |
П |
М |
М |
Г |
В |
Т |
Р |
Щ |
О |
|
Я |
Ы |
Щ |
В |
Ф |
Н |
К |
К |
Б |
А |
Р |
О |
Ч |
М |
М |
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
К |
К |
Э |
О |
И |
Н |
У |
Ц |
Ш |
Р |
Ю |
Е |
И |
И |
С |
|
О |
Б |
Т |
Н |
С |
Ч |
Ь |
Э |
Ф |
В |
К |
Н |
Н |
Х |
Ц |
|
участок |
Г |
Ф |
П |
У |
Щ |
Э |
Я |
Ц |
Д |
М |
П |
П |
Ч |
Ш |
И |
|
и.с.1 |
Д |
Я |
Г |
К |
Н |
П |
Ж |
Ф |
Ы |
Я |
Я |
З |
И |
Ш |
Ь |
|
А |
Д |
Л |
О |
Р |
З |
Х |
Э |
А |
А |
И |
К |
Щ |
Ы |
Т |
|
О |
Ф |
Ч |
Щ |
С |
Я |
Ж |
К |
К |
Т |
У |
Г |
Е |
Ы |
З |
|
Т |
Х |
Ч |
П |
Э |
Д |
З |
З |
Р |
С |
Б |
Г |
Щ |
Е |
Е |
Из таблиц видно, что осмысленными являются варианты:
|
и.с.1 |
= |
К |
О |
Г |
Д |
А |
О |
Т |
. |
. |
. |
. |
. |
. |
. |
К |
О |
Р |
А |
Б |
Л |
И |
|
и.с.2 |
= |
К |
О |
Р |
А |
Б |
Л |
И |
. |
. |
. |
. |
. |
. |
. |
В |
Е |
Ч |
Е |
Р |
О |
М
|
|
Естественно предположить, что в первом исходном сообщении речь
идет об отплытии кораблей. Предположив, что неизвестным
участком первого исходного сообщения является
подходящая по смыслу часть слова
ОТПЛЫВАЮТ, находим неизвестную часть второго исходного
сообщения: слово ОТХОДЯТ.
2.6. Каждую букву шифрованного сообщения расшифруем в трех
вариантах, предполагая последовательно, что соответствующая буква
шифрующей последовательности есть буква А, Б или буква
В:
|
шифрованное сообщение |
Р |
Б |
Ь |
Н |
П |
Т |
С |
И |
Т |
С |
Р |
Р |
Е |
З |
О |
Х |
|
вариант А |
П |
А |
Щ |
М |
О |
С |
Р |
З |
С |
Р |
П |
П |
Д |
Ж |
Н |
Ф |
|
вариант Б |
О |
Я |
Ш |
Л |
Н |
Р |
П |
Ж |
Р |
П |
О |
О |
Г |
Е |
М |
У |
|
вариант В |
Н |
Ю |
Ч |
К |
М |
П |
О |
Е |
П |
О |
Н |
Н |
В |
Д |
Л |
Т |
Выбирая из каждой колонки полученной таблицы ровно по одной
букве, находим осмысленное сообщение
НАШКОРРЕСПОНДЕНТ, которое и является искомым.
Замечание. Из полученной таблицы можно было
найти такое исходное сообщение как
которое представляется не менее осмысленным, чем приведенное выше. А
если предположить одно искажение в шифрованном сообщении (скажем, в
качестве 11-й буквы была бы принята не буква Р, а буква П), то, наряду с правильным вариантом, можно получить и такой:
Число всех различных вариантов исходных
сообщений без ограничений на осмысленность равно  или
43046721, т.е. более 40 миллионов! или
43046721, т.е. более 40 миллионов!
Next: ...к задачам третьей олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам первой олимпиады
Contents: Содержание
| 
