Next: ...к задачам седьмой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам пятой олимпиады
Contents: Содержание
6.1. Так как каждый из 1997 абонентов связан ровно с 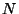 другими, то общее число направлений связи равно
другими, то общее число направлений связи равно  . Отсюда общее
число связанных пар абонентов равно . Отсюда общее
число связанных пар абонентов равно  , так как каждая связанная
пара имеет ровно 2 направления связи. Поскольку число , так как каждая связанная
пара имеет ровно 2 направления связи. Поскольку число  должно
быть целым, а число 1997 - нечетное, то число должно
быть целым, а число 1997 - нечетное, то число 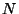 должно быть четным. должно быть четным.
Докажем, что для каждого  существует система связи из
1997 абонентов, в которой каждый связан ровно с существует система связи из
1997 абонентов, в которой каждый связан ровно с 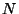 другими. В самом
деле, расположив всех абонентов на окружности и связав каждого из них с другими. В самом
деле, расположив всех абонентов на окружности и связав каждого из них с
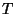 ближайшими к нему по часовой стрелке и с ближайшими к нему против
часовой стрелки, получим пример такой сети связи. ближайшими к нему по часовой стрелке и с ближайшими к нему против
часовой стрелки, получим пример такой сети связи.
6.2. Покажем, что на диагонали присутствуют все числа от 1 до
1997. Пусть число
 не стоит на диагонали. Тогда,
в силу симметрии таблицы, число не стоит на диагонали. Тогда,
в силу симметрии таблицы, число  встречается четное количество раз.
С другой стороны, так как число встречается четное количество раз.
С другой стороны, так как число  по одному разу встречается в каждой
строке, всего в таблице чисел по одному разу встречается в каждой
строке, всего в таблице чисел  нечетное количество (1997). Получили
противоречие. нечетное количество (1997). Получили
противоречие.
Всего на диагонали 1997 клеток, поэтому каждое число из
множества
 встретится на диагонали ровно по одному разу.
Вычисляя сумму арифметической прогрессии, находим ответ.
встретится на диагонали ровно по одному разу.
Вычисляя сумму арифметической прогрессии, находим ответ.
Ответ: 1995003.
6.3. Ответ:
ШЕСТАЯОЛИМПИАДАПОКРИПТОГРАФИИПОСВЯЩЕНАСЕМИДЕСЯТИ
ПЯТИЛЕТИЮСПЕЦИАЛЬНОЙСЛУЖБЫРОССИИ
Указание. Пусть некоторая буква  при зашифровании
первым способом заменялась на букву при зашифровании
первым способом заменялась на букву  . Тогда количество повторов
буквы . Тогда количество повторов
буквы  в первой криптограмме будет равно числу повторов буквы в первой криптограмме будет равно числу повторов буквы
 во второй криптограмме. во второй криптограмме.
6.4. а) Определим моменты остановок после начала шифрования. Для
этого каждой букве русского алфавита припишем ее порядковый номер:
А - 0,
Б - 1, и т.д. Тогда буквам из шифруемого слова будут
соответствовать номера: О - 15, Л - 12, И - 9, М - 13, П -16, А - 0, Д - 4. Моменты остановок будем указывать числом одношаговых (на один
зубец) поворотов I колеса до соответствующей остановки.
|
# остановки |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Буква I колеса |
О |
Л |
И |
М |
П |
И |
А |
Д |
А |
|
Число одношаговых поворотовот начала до остановки |
15 |
45 |
75 |
79 |
82 |
108 |
132 |
136 |
165 |
|
Цифра II колеса |
5 |
5 |
5 |
1 |
8 |
2 |
8 |
4 |
5 |
|
Цифра III колеса |
1 |
2 |
5 |
2 |
5 |
3 |
6 |
3 |
4 |
|
Искомый шифртекст: 515355128523864354
б) Пусть  - количество одношаговых поворотов I
колеса от начала до остановки с номером - количество одношаговых поворотов I
колеса от начала до остановки с номером  , ,  , ,
 - цифра, на которую указывает стрелка II
колеса в момент остановки с номером - цифра, на которую указывает стрелка II
колеса в момент остановки с номером  , ,
 - цифра III колеса, на которую указывает
стрелка III колеса в момент остановки с номером - цифра III колеса, на которую указывает
стрелка III колеса в момент остановки с номером  . .
Тогда, учитывая, что начальное положение стрелок соответствует
букве А на первом колесе и 0 на II и III колесах, справедливы равенства

для подходящих неотрицательных целых чисел  и и  . .
Заметим, что
 . Отсюда справедливы равенства . Отсюда справедливы равенства

Подставляя эти значения в равенства (1) и (2),
получим

Следовательно,

Правая и левая части делятся на 70, то есть
имеют вид  для подходящего неотрицательного целого для подходящего неотрицательного целого  . Поэтому . Поэтому

Подставляя  в (1), получим в (1), получим

Учитывая условие
 и то, что остановка
колеспроисходит в момент первого появления шифруемой буквы
под стрелкой I колеса, имеем и то, что остановка
колеспроисходит в момент первого появления шифруемой буквы
под стрелкой I колеса, имеем
6.5. Указание. Рассмотрим некоторую расстановку ненулевых цифр
на окружности. Упорядоченную пару  соседних цифр на этой
окружности назовем 1-соседней, если соседних цифр на этой
окружности назовем 1-соседней, если  является соседней с является соседней с  по
часовой стрелке. Пару по
часовой стрелке. Пару  назовем 2-соседней, если существует
цифра назовем 2-соседней, если существует
цифра  , для которой пары , для которой пары  и и  являются 1-соседними. являются 1-соседними.
Каждой расстановке ненулевых цифр на окружности однозначно
соответствует цепочка 1-соседних пар вида:  , ,
 , ,
 , ..., , ...,  , ,  ,
которой, в свою очередь, однозначно соответствует цепочка 2-соседних
пар вида: ,
которой, в свою очередь, однозначно соответствует цепочка 2-соседних
пар вида:

где
 и и  при при  . .
Если из цепочки  удалить любую пару, то по
оставшимся парам она восстанавливается однозначно. удалить любую пару, то по
оставшимся парам она восстанавливается однозначно.
Если из цепочки  удалить две соседние пары, то она также
восстанавливается однозначно. удалить две соседние пары, то она также
восстанавливается однозначно.
Удаление из  любых трех пар приводит к
неоднозначности восстановления цепочки любых трех пар приводит к
неоднозначности восстановления цепочки  . В этом можно убедиться,
рассмотрев следующие фрагменты цепочки вида . В этом можно убедиться,
рассмотрев следующие фрагменты цепочки вида  : :

Таким образом, при наличии двух указанных в условии задачи цифровых
текстов нам будут известны некоторые 2-соседние пары, в которых первая
цифра берется из первой криптограммы, а вторая - из второй. Поэтому с
учетом вышесказанного получаем условие однозначного восстановления
порядка расстановки цифр на данной окружности.
Ответ:
для однозначного восстановления расстановки цифр на окружности
необходимо и достаточно, чтобы в одном из цифровых текстов было не
менее 7 ненулевых цифр (это соответствует удалению из цепочки
2-соседних пар вида  не более двух из них). не более двух из них).
6.6. Последовательность остатков
от деления
чисел
 на 24 -
периодическая с периодом 2, так как для любого
натурального на 24 -
периодическая с периодом 2, так как для любого
натурального  справедливо: справедливо:

Кроме того,
 кратно 24, то есть
остатки у кратно 24, то есть
остатки у  и и  равны. равны.
6.7. Ответ:  ; все решения имеют вид ; все решения имеют вид
 , ,
 . .
Указание. При  рассматриваемое уравнение равносильно рассматриваемое уравнение равносильно
 , которое имеет не более двух решений. , которое имеет не более двух решений.
При  из графика функции в левой части уравнения видно,
что если из графика функции в левой части уравнения видно,
что если  , число решений будет четным, поэтому не может
быть равно 1997. Если , число решений будет четным, поэтому не может
быть равно 1997. Если
 , то уравнение имеет ровно
2 решения. Если же , то уравнение имеет ровно
2 решения. Если же  , то уравнение имеет ровно 1997 решений. , то уравнение имеет ровно 1997 решений.
Next: ...к задачам седьмой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам пятой олимпиады
Contents: Содержание
| 
