Next: ...к задачам восьмой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам шестой олимпиады
Contents: Содержание
7.1. Для того, чтобы сохранилась связь при выходе из строя
любых двух узлов, необходимо, чтобы в каждый узел входило не менее трех
линий связи. Ситуация
недопустима, ибо при выходе из строя узлов  и и 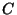 узел узел  становится недоступным. Значит, всего линий должно быть не менее
становится недоступным. Значит, всего линий должно быть не менее
 . .
Вот два примера, удовлетворяющие условиям задачи с 15-ю линиями связи:
Приведем
доказательство
для первого примера.
Если вышли из строя
два узла на одном
пятиугольнике, то связь сохранится через другие пятиугольники. Если
вышли из строя по одному узлу на разных пятиугольниках, то связь
сохранится по линиям, соединяющим эти пятиугольники.
Ответ: 15.
7.2. Процедура зашифрования может быть полностью описана
квадратной таблицей  . На пересечении строки с номером . На пересечении строки с номером 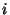 и
столбца с номером и
столбца с номером 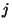 записываем цифру, в которую при зашифровании
переходит цифра записываем цифру, в которую при зашифровании
переходит цифра 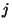 , если она стоит в пароле после цифры , если она стоит в пароле после цифры 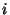 . Из
однозначности расшифрования следует, что в каждой строке каждая цифра
встречается ровно один раз. . Из
однозначности расшифрования следует, что в каждой строке каждая цифра
встречается ровно один раз.
Обозначим через
 и и  зашифрованные пароли и два известных пароля в порядке, определяемом
условием задачи. Процедура зашифрования сохраняет длину, поэтому
зашифрованные пароли и два известных пароля в порядке, определяемом
условием задачи. Процедура зашифрования сохраняет длину, поэтому  и
и  не могут соответствовать ни не могут соответствовать ни  , ни , ни  . Предположив, что . Предположив, что
 соотвествует соотвествует  , получим часть таблицы, в которой в одной
строке две одинаковые цифры. Это означает, что предположение неверно.
Составляя таблицы, убеждаемся, что , получим часть таблицы, в которой в одной
строке две одинаковые цифры. Это означает, что предположение неверно.
Составляя таблицы, убеждаемся, что  не шифруется ни в не шифруется ни в  ,
ни в ,
ни в  , ни в , ни в  . В результате таких рассуждений остается
только один
вариант перехода . В результате таких рассуждений остается
только один
вариант перехода  , ,  . Заполнение таблицы
будет следующим: . Заполнение таблицы
будет следующим:
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
|
|
|
|
|
|
|
5 |
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
2 |
4 |
3 |
7 |
|
|
|
|
8 |
|
|
|
3 |
|
7 |
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
4 |
|
|
|
|
|
8 |
|
|
1 |
9 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
|
|
6 |
|
|
|
|
|
5 |
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
2 |
4 |
3 |
7 |
0 |
6 |
2 |
5 |
8 |
9 |
|
|
3 |
3 |
7 |
|
|
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
3 |
7 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
4 |
|
|
|
|
|
8 |
|
|
1 |
9 |
|
|
|
|
|
|
|
9 |
|
|
1 |
|
|
|
|
|
|
|
|
Очевидно, что в строке с номером 2 в последней клетке стоит 1. Знание этой
таблицы позволяет однозначно расшифровать  : получится 5830829.
Пароли, соответствующие : получится 5830829.
Пароли, соответствующие  , ,  , ,  , ,  ,
восстанавливаются не полностью. ,
восстанавливаются не полностью.
Ответ: полностью можно расшифровать только 5393511, получится
5830829.
7.3. Сообщение состоит из  буквы. Поэтому буквы. Поэтому  или
или  (при (при  и и  - получается нечитаемый текст). При - получается нечитаемый текст). При
 не получается осмысленного текста при всех шести возможных
вариантах перестановки букв
( не получается осмысленного текста при всех шести возможных
вариантах перестановки букв
( , ,  ). Рассмотрим случай ). Рассмотрим случай  : :
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
Б |
Т |
И |
П |
Ч |
Ь |
Л |
О |
Я |
Ч |
Ы |
Ь |
Т |
О |
Т |
П |
У |
|
Н |
Т |
Н |
О |
Н |
З |
Л |
Ж |
А |
Ч |
О |
Ь |
О |
Т |
У |
Н |
И |
|
У |
Х |
Н |
И |
П |
П |
О |
Л |
О |
Ь |
Ч |
О |
Е |
Л |
О |
Л |
С
|
|
Соседние буквы при перестановке переходят в буквы, отстоящие друг
от друга на одинаковое расстояние: буква на  -м месте переходит на
место, определяемое остатком от деления -м месте переходит на
место, определяемое остатком от деления  на 17, а буква на на 17, а буква на
 -м месте - на место, определяемое остатком от деления -м месте - на место, определяемое остатком от деления
 на 17. Это верно для любого на 17. Это верно для любого  . Поэтому есть всего 16
вариантов переходов соседних букв (исходный текст нечитаем), которые
определяют однозначно переходы всех остальных букв. Перебирая их,
получаем нечитаемые тексты во всех случаях, кроме одного, который дает
текст: . Поэтому есть всего 16
вариантов переходов соседних букв (исходный текст нечитаем), которые
определяют однозначно переходы всех остальных букв. Перебирая их,
получаем нечитаемые тексты во всех случаях, кроме одного, который дает
текст:
|
Ч |
И |
Т |
Ь |
П |
Я |
Т |
Ь |
Ч |
Т |
О |
Б |
Ы |
П |
О |
Л |
У |
|
Ч |
Н |
О |
З |
Н |
А |
Т |
Ь |
Н |
У |
Ж |
Н |
О |
О |
Т |
Л |
И |
|
Ь |
Н |
Е |
П |
Л |
О |
Х |
О |
П |
О |
Л |
У |
Ч |
И |
Л |
О |
С
|
|
Из трех вариантов начала текста легко определяется истинный вариант.
Ответ:
|
ЧТОБЫПОЛУЧИТЬПЯТЬНУЖНООТЛИЧНОЗНАТЬПОЛУЧИЛОСЬНЕПЛОХО |
7.4. Последовательность обхода доски показана на
рисунке:
Ответ:
Кавалергардов век недолог
И потому так сладок он.
Труба трубит, откинут полог...
7.5. Из однородности всех членов следует, что неравенство
эквивалентно неравенству
 при условии при условии
 , ,  , ,  , ,  . .
Пусть  - минимальное из чисел - минимальное из чисел  (
( ) и ) и  . Тогда . Тогда

Находим минимум квадратного трехчлена с
параметром  и положительным коэффициентом при
и положительным коэффициентом при  . Минимум
достигается в точке . Минимум
достигается в точке  , при этом значение , при этом значение  будет
положительным. будет
положительным.
7.6. Если мелом с квадратным сечением нарисовать на доске
отрезок прямой так, чтобы стороны сечения были параллельны
краям доски, то площадь полученной линии будет равна площади
ступенчатой линии с такими же концами (см. рис. 20).
Если на доске нарисовать некоторый (выпуклый) многоугольник, то
найдутся такие граничные ``точки'' этого многоугольника, которые
являются ближайшими к одному из краев доски. Площадь границы
прямоугольника, содержащей все такие ``точки'', равна площади
границы нарисованного выпуклого многоугольника (см.
рис. 21).
Такой прямоугольник назовем окаймляющим. Ясно, что
площадь окаймляющего прямоугольника не меньше площади соответствующего
многоугольника. Значит, для любого многоугольника данной площади
найдется прямоугольник такой же площади, но с площадью границы не большей,
чем площадь границы исходного многоугольника.
Если многоугольник со сторонами  и и  имеет площадь
10000 см имеет площадь
10000 см , то площадь его границы равна , то площадь его границы равна

Минимум достигается в случае, когда возводимое в квадрат выражение
равно 0. В этом случае  , что влечет , что влечет  . Таким образом,
наименьшую площадь границы, равную 404 см . Таким образом,
наименьшую площадь границы, равную 404 см , имеет квадрат со
стороной 1 м. , имеет квадрат со
стороной 1 м.
Ответ: квадрат со стороной 1 м; площадь его границы -
404 см . .
7.7. Если группа цифр, из которой образуются числа,
состоит из  цифр, то существует ровно цифр, то существует ровно  различных чисел, для
записи которых используются все цифры группы ровно по одному разу.
Группу из различных чисел, для
записи которых используются все цифры группы ровно по одному разу.
Группу из  цифр будем обозначать цифр будем обозначать  . .
Поскольку в сообщении отсутствуют цифры 2 и 9, эти цифры образуют
либо две группы по одной цифре, либо одну группу из двух цифр. В обоих случаях
эти цифры могут быть использованы для зашифрования ровно двух букв алфавита.
Так как  , то , то
 . .
Если  , то из сообщения находим: , то из сообщения находим:
а)
 , ,  , ,  либо либо
б)
 , ,  , ,  . .
| | |
Случай а |
Случай б |
|
Случай а |
Случай б |
|
Случай а |
Случай б |
|
| |
А |
2 (4) |
0 |
К |
1738 |
1738 |
Х |
7183 |
7183 |
|
| |
Б |
4 (29) |
2 (29) |
Л |
1783 |
1783 |
Ц |
7318 |
7318 |
|
| |
В |
9 (56) |
9 (92) |
М |
1837 |
1837 |
Ч |
7381 |
7381 |
|
| |
Г |
56 (65) |
456 |
Н |
1873 |
1873 |
Ш |
7813 |
7813 |
|
| |
Д |
65 (92) |
465 |
О |
3178 |
3178 |
Щ |
7831 |
7831 |
|
| |
Е |
506 |
546 |
П |
3187 |
3187 |
Ъ |
8137 |
8137 |
|
| |
 |
605 |
564 |
Р |
3718 |
3718 |
Ы |
8173 |
8173 |
|
| |
Ж |
650 |
645 |
С |
3781 |
3781 |
Ь |
8317 |
8317 |
|
| |
З |
650 |
654 |
Т |
3817 |
3817 |
Э |
8371 |
8371 |
|
| |
И |
1378 |
1378 |
У |
3871 |
3871 |
Ю |
8713 |
8713 |
|
| |
Й |
1387 |
1387 |
Ф |
7138 |
7138 |
Я |
8731 |
8731 |
|
|
Сообщение после расшифрования имеет вид:
а) ЯАЗЧ или б) ЯДАЧ, т.е. не читается.
Если  , то из сообщения находим , то из сообщения находим
 , ,
 . В этом случае таблица замены букв числами имеет
вид: . В этом случае таблица замены букв числами имеет
вид:
|
А |
1 |
 |
465 |
Л |
783 |
С |
4560 |
Ч |
5460 |
Э |
6450 |
|
Б |
2(29) |
Ж |
546 |
М |
837 |
Т |
4605 |
Ш |
5604 |
Ю |
6504 |
|
В |
9(92) |
З |
564 |
Н |
873 |
У |
4650 |
Щ |
5640 |
Я |
6540 |
|
Г |
378 |
И |
645 |
О |
4056 |
Ф |
5046 |
Ъ |
6045 |
|
|
|
Д |
387 |
Й |
654 |
П |
4065 |
Х |
5064 |
Ы |
6054 |
|
|
| Е |
456 |
К |
738 |
Р |
4506 |
Ц |
5406 |
Ь |
6405 |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
Сообщение легко прочитать: НАУКА.
Next: ...к задачам восьмой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам шестой олимпиады
Contents: Содержание
| 
