Next: ...к задачам девятой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам седьмой олимпиады
Contents: Содержание
8.1.
Проведем прямые, проходящие через точки пересечения границ сложенной
ленты параллельно ее краям. Очевидно, что тогда лента разобьется на
равные равносторонние треугольники. Отметим цифрой 0 все просветы, а
цифрой 2 все треугольники, которые получились наложением друг на друга
двух треугольников в сложенной ленте. Построим дополнительно ряд
треугольников вне эмблемы, как показано на рисунке 22. В
полученной фигуре
число треугольников, отмеченных цифрой 2, равно числу треугольников,
отмеченных цифрой 0. Поэтому площадь всей ленты равна площади трапеции
 . Количества треугольников в горизонтальных рядах . Количества треугольников в горизонтальных рядах  являются 9 последовательными членами арифметической прогрессии с первым
членом, равным 3 (нижний ряд), и разностью 2. Следовательно, общее
число треугольников равно
являются 9 последовательными членами арифметической прогрессии с первым
членом, равным 3 (нижний ряд), и разностью 2. Следовательно, общее
число треугольников равно

Если  - ширина ленты, то площадь одного равностороннего
треугольника с высотой - ширина ленты, то площадь одного равностороннего
треугольника с высотой  равна равна

С другой стороны, если длина прямоугольника, полученного
послеразрезания ленты, равна  , то , то  .
Отсюда находим искомую величину: .
Отсюда находим искомую величину:  . .
Ответ:  . .
8.2.
Последовательность из  нулей или нулей или  единиц обозначим соответственно
через единиц обозначим соответственно
через  или или  . Тогда шифрование каждого знака сообщения
состоит в замене . Тогда шифрование каждого знака сообщения
состоит в замене
 |
(1) |
В зашифрованном сообщении все серии из единиц имеют длину
 для первого
способа и длину для первого
способа и длину  для второго способа, поэтому, для совпадения
результатов зашифрования необходимо, чтобы для второго способа, поэтому, для совпадения
результатов зашифрования необходимо, чтобы
 |
(2) |
Теперь легко получить, что в сообщении должно быть одинаковое число
нулей и единиц.
Пусть  - число нулей в сообщении. Тогда число нулей в
зашифрованном I способом сообщении равно - число нулей в сообщении. Тогда число нулей в
зашифрованном I способом сообщении равно  , а II
способом - , а II
способом -  . Таким образом, . Таким образом,
 |
(3) |
Из (1) видно, что сообщение должно начинаться с нуля и
оканчиваться единицей. Пусть перед первой единицей сообщения
расположено  нулей. Тогда первые нулей. Тогда первые  знаков сообщения
представляются при шифровании в виде: знаков сообщения
представляются при шифровании в виде:
 |
(4) |
При  получаем необходимость равенства получаем необходимость равенства  , а
значит, с учетом (3) - равенства , а
значит, с учетом (3) - равенства  . .
При  получаем условия: получаем условия:

Подставляя  в (3), получаем равенство
в (3), получаем равенство  ,
которое при натуральных ,
которое при натуральных  , ,  и
и  возможно лишь в случае возможно лишь в случае  .
Следовательно, .
Следовательно,  ,
а значит, с учетом (3) ,
а значит, с учетом (3)  . .
Таким образом, при  необходимы условия необходимы условия
 , ,
 ,
где ,
где  - натуральное. Из (4) следует, что
сообщение должно иметь вид - натуральное. Из (4) следует, что
сообщение должно иметь вид
 , где число нулей и число
единиц равно , где число нулей и число
единиц равно  . .
Ответ:
При  , ,  , ,  сообщения вида
сообщения вида  шифруются одинаково. шифруются одинаково.
При  , ,
 ,
где ,
где  - натуральное, сообщения вида - натуральное, сообщения вида
 (группы из
(группы из  нулей и нулей и  единиц) шифруются одинаково. единиц) шифруются одинаково.
Примечание. Первый ответ не является частным случаем второго при
 . .
8.3. Естественно предположить, что все члены оргкомитета
родились в ХХ веке. Отсюда сразу замечаем, что на 3, 7, 11, 15, 19 и
23 местах последовательности простых чисел расположены числа 11, 17,
47, 53, 83 и 89 соответственно.
Выясним, какие числа являются соседними с указанными шестью
числами. Для этого составим таблицу их возможных ``соседей''. В
соответствии с условием имеем:
|
число |
соседи |
|
11 |
13, 19, 43, 7, 3 |
|
17 |
13, 19 |
|
47 |
79, 43, 31 |
|
53 |
61, 37 |
|
83 |
79, 67, 19 |
|
89 |
97, 73. |
|
Учитывая, что первая цифра в номере месяца принимает значения
только 0 или 1, построим следующую таблицу:
| | 15 |
02 |
20 |
45 |
42 |
13 |
26 |
67 |
44 |
30 |
56 |
82 |
53 |
33 |
62 |
32 |
73 |
63 |
92 |
49 |
75 |
70 |
98 |
49 |
|
| | |
|
19 |
|
|
|
19 |
|
|
|
19 |
|
|
|
19 |
|
|
|
19 |
|
|
|
19 |
|
|
| | |
|
11 |
|
|
|
17 |
|
|
31 |
47 |
|
|
37 |
53 |
61 |
|
67 |
83 |
|
|
73 |
89 |
97 |
|
| | |
03 |
|
03 |
|
13 |
|
13 |
|
|
|
43 |
|
|
|
|
|
|
|
19 |
|
|
|
|
|
| | |
07 |
|
07 |
|
19 |
|
19 |
|
|
|
79 |
|
|
|
|
|
|
|
79 |
|
|
|
|
|
| | |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где в первой строке расположено шифрованное сообщение, во второй
строке - известные участки исходного сообщения, в третьей
строке - ставшие
известными участки ключевой последовательности, в остальных
строках -
возможные варианты ключевой последовательности в соответствующих
позициях. При составлении таблицы учитывалось, что каждое число должно
встретиться ровно один раз. Позиции чисел 31, 37, 67, 73 определяются
однозначно. Их расположение однозначно определяет места для простых
чисел 61 и 97.
Снова выпишем известные числа последовательности
простых чисел и варианты для их соседей
(первые две строки таблицы на этом шаге не понадобятся):
| | |
|
11 |
|
|
|
17 |
|
|
31 |
47 |
|
|
37 |
53 |
61 |
|
67 |
83 |
|
|
73 |
89 |
97 |
|
|---|
| | |
03 |
|
03 |
|
13 |
|
13 |
|
|
|
43 |
|
|
|
|
|
|
|
19 |
|
|
|
|
|
| | |
07 |
|
07 |
|
19 |
|
19 |
|
|
|
79 |
|
|
|
|
|
|
|
79 |
|
|
|
|
|
| | |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возможные соседи для числа 61 - лишь 59 и 29, а для 67 - лишь
59 и 3. Поэтому между 61 и 67 может находиться только число 59.
Возможными соседями для числа 73 являются 89, 71 и 41. Ни одно из этих
чисел не может быть соседом для 19, а для 79 может быть только 71.
Таким образом, однозначно определяется расположение чисел 71 и 79. Для
числа 47 остался только один кандидат в соседи справа - число 43.
Общим соседом для 43 и 37 может быть только 41. Скорректируем таблицу с
учетом сделанных выводов:
| | |
|
11 |
|
|
|
17 |
|
|
31 |
47 |
43 |
41 |
37 |
53 |
61 |
59 |
67 |
83 |
79 |
71 |
73 |
89 |
97 |
|
|---|
| | |
03 |
|
03 |
|
13 |
|
13 |
29 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
07 |
|
07 |
|
19 |
|
19 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | |
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Участок последовательности  имеет только два
варианта доопределения: (а) имеет только два
варианта доопределения: (а)
 и (б) и (б)
 .
Рассмотрим оба случая. .
Рассмотрим оба случая.
а) Выпишем фрагмент таблицы для первого случая:
| | |
|
11 |
|
|
13 |
17 |
19 |
23 |
31 |
|
|---|
| | |
03 |
|
03 |
|
|
|
|
|
|
|
| | |
07 |
|
07 |
|
|
|
|
|
|
|
Очевидно, что числа 3 и 7 должны обязательно быть соседними с числом
11. Число 29 еще не встречалось, значит оно должно располагаться либо
на первом месте, либо на пятом. И то и другое невозможно, так как в
обоих позициях оно является соседом либо для числа 3, либо для числа 7,
что не соответствует условию (отличие соседних чисел на степень
двойки). Следовательно, рассматриваемый случай невозможен.
б) Выпишем фрагмент таблицы для второго случая:
| | 05 |
|
11 |
|
23 |
19 |
17 |
13 |
29 |
31 |
|
|---|
| | |
03 |
|
03 |
|
|
|
|
|
|
|
| | |
07 |
|
07 |
|
|
|
|
|
|
|
Очевидно, что числа 3 и 7 должны обязательно быть соседями для числа
11. Число 5 может попасть только на первую позицию (т.к. оно не может
находиться рядом с 19). Значит, в пятой позиции должно быть число 23.
Ясно, что числа 3 и 7 теперь расставляются однозначно.
Таким образом, приходим к выводу, что возможен всего один вариант
ключевой последовательности. Получим окончательный вариант таблицы и
найдем ответ:
| | 15 |
02 |
20 |
45 |
42 |
13 |
26 |
67 |
44 |
30 |
56 |
82 |
53 |
33 |
62 |
32 |
73 |
63 |
92 |
49 |
75 |
70 |
98 |
49 |
|
| | 10 |
09 |
19 |
48 |
29 |
04 |
19 |
54 |
25 |
09 |
19 |
49 |
12 |
06 |
19 |
71 |
24 |
06 |
19 |
70 |
04 |
07 |
19 |
52 |
|
| | 05 |
03 |
11 |
07 |
23 |
19 |
17 |
13 |
29 |
31 |
47 |
43 |
41 |
37 |
53 |
61 |
59 |
67 |
83 |
79 |
71 |
73 |
89 |
97 |
|
Ответ: 10.09.1948 29.04.1954 25.09.1949 12.06.1971
24.06.1970 04.07.1952
8.4.
Занумеруем горизонтали и вертикали квадрата натуральными числами от 1
до 13 сверху вниз и слева направо соответственно. Тогда каждая клетка
квадрата однозначно определяется парой чисел  , где , где 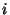 -
номер горизонтали, а -
номер горизонтали, а 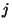 - номер вертикали, в которых находится
клетка. - номер вертикали, в которых находится
клетка.
Расстояние между центром клетки  и центром клетки и центром клетки  равно
равно
 .
Заметим, что .
Заметим, что
 и
и
 .
Обозначим .
Обозначим  , ,  , ,
 .
Тогда .
Тогда  - число натуральное, если - число натуральное, если
 .
Отсюда получаем, что .
Отсюда получаем, что


В
общем случае, если  , то , то

Ясно, что  и и  должны быть одинаковой четности. По условию, должны быть одинаковой четности. По условию,
 ,
поэтому искомыми решениями будут только пары ,
поэтому искомыми решениями будут только пары

Клетку  назовем существенной для клетки назовем существенной для клетки  , если
выполнено условие , если
выполнено условие
 .
Ясно, что цвет данной клетки менялся лишь тогда,
когда Криптоша находился в какой-либо существенной для нее клетке. А
так как в каждой клетке Криптоша побывал ровно 1999 раз (нечетное
число), то цвет данной клетки изменился, если общее число существенных
для нее клеток нечетно. .
Ясно, что цвет данной клетки менялся лишь тогда,
когда Криптоша находился в какой-либо существенной для нее клетке. А
так как в каждой клетке Криптоша побывал ровно 1999 раз (нечетное
число), то цвет данной клетки изменился, если общее число существенных
для нее клеток нечетно.
Для определения четности числа всех существенных клеток для данной
клетки воспользуемся тем, что у симметричных клеток относительно той
или иной диагонали квадрата или относительно центрального вертикального
или центрального горизонтального рядов эти числа будут одинаковы.
Это, в частности, означает, что достаточно определить указанную
четность только для клеток  , где , где
 , ,
 (этих клеток 15, занумеруем их,
как показано на рис. 23). (этих клеток 15, занумеруем их,
как показано на рис. 23).
Рис. 23.
Для клетки 1 жирными линиями выделена зона асимметрии.
Серым цветом отмечены
клетки верхнего левого угла  , меняющие свой цвет , меняющие свой цвет
|
Кроме того, отметим, что у каждой из клеток на диагоналях квадрата, а
также у каждой из клеток центрального вертикального и горизонтального
рядов обязательно будет четное число существенных для нее клеток.
Зоной асимметрии для той или иной
клетки мы назовем множество тех клеток, которые в пределах исходного
квадрата не имеют клеток, симметричных относительно вертикального,
горизонтального и правого диагональных рядов, содержащих данную
клетку. Ясно, что для данной клетки число существенных клеток, не
лежащих в ее зоне асимметрии, четно.
На рис. 23 показана зона асимметрии
для клетки 1, а также все клетки верхнего левого угла  ,
меняющие свой цвет. ,
меняющие свой цвет.
Ответ на рис. 24.
8.5.
При решении этого уравнения надо учитывать возможные ограничения:
 , ,  , ,
 , ,  . Поэтому целесообразно выделить их сразу. . Поэтому целесообразно выделить их сразу.
1. Пусть  , ,  . Уравнение имеет вид . Уравнение имеет вид
 , то есть , то есть 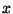 - любое число. - любое число.
2. Пусть  , ,  . Уравнение имеет вид . Уравнение имеет вид
 , или , или  , то есть не
имеет решений. , то есть не
имеет решений.
3. Аналогично, при  , ,  нет решений. нет решений.
4. При  , ,  удобно рассмотреть три случая:
а) удобно рассмотреть три случая:
а)  ,
b) ,
b)  , c) , c)  . .
a)  : :
 , ,
 , ,
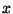 - любое,
кроме - любое,
кроме  . .
b)  : :
 , ,
 , ,
 , ,
 ,
решений нет. ,
решений нет.
c)  : :
![\begin{gather*}
\frac{a}{1-bx}=\frac{b}{1-ax},
\qquad x\ne\frac{1}{a}, x\ne\fr...
...\frac{1}{a},\ [2pt]
x=\frac{(a-b)ab}{ab(a^2-b^2}=\frac{1}{a+b}.
\end{gather*}](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1688.gif)
Ответ. При  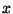 - любое число. - любое число.
При 
 . .
При  или или  или
или  решений нет. решений нет.
При

 . .
8.6. Число  представляет собой сумму кубов, сумму
пятых степеней, а также из него можно выделить полный квадрат. Каждое
из этих представлений позволяет найти некоторые делители исходного
числа: представляет собой сумму кубов, сумму
пятых степеней, а также из него можно выделить полный квадрат. Каждое
из этих представлений позволяет найти некоторые делители исходного
числа:

Таким образом, установлено, что среди простых делителей числа  содержатся 41, 13, 5. Непосредственной проверкой получаем равенство
содержатся 41, 13, 5. Непосредственной проверкой получаем равенство
 . .
Осталось проверить, что 1321 - простое число. Для этого достаточно
показать, что 1321 не делится ни на одно простое число, меньшее 37
( , ,  ). ).
Ответ:
 . .
Next: ...к задачам девятой олимпиады
Up: 7.6. Указания и решения
Previous: ...к задачам седьмой олимпиады
Contents: Содержание
|

