Next: Литература к главе 7
Up: 7.6. Указания и решения
Previous: ...к задачам восьмой олимпиады
Contents: Содержание
9.1.
а) Для доказательства достаточно указать хотя бы одну
последовательность из 33 различных букв, сумма которой с русским
алфавитом из 33 букв не содержит одинаковых букв. В качестве искомой
последовательности возьмем сам алфавит. Докажем, что сумма алфавита с
самим собой не содержит одинаковых букв. Пусть  и и  -
порядковые номера различных букв алфавита. Тогда по определению
сложения букв достаточно показать, что числа -
порядковые номера различных букв алфавита. Тогда по определению
сложения букв достаточно показать, что числа  и и  имеют разные
остатки от деления на 33. В самом деле, если бы они были одинаковы, то
число имеют разные
остатки от деления на 33. В самом деле, если бы они были одинаковы, то
число  делилось бы на 33 без остатка. В силу того что делилось бы на 33 без остатка. В силу того что
 , разность , разность  также делилась бы на 33 без
остатка, что невозможно. Утверждение пункта а) доказано. также делилась бы на 33 без
остатка, что невозможно. Утверждение пункта а) доказано.
Замечание. Утверждение пункта а) остается в силе для любого
алфавита из нечетного числа букв.
б) При сложении двух последовательностей сумма порядковых номеров всех
букв получаемой при этом последовательности и сумма порядковых номеров
всех букв обоих слагаемых имеет один и тот же остаток от деления на 26.
Значит, разность упомянутых сумм должна делиться на 26 без остатка.
Докажем утверждение пункта б) методом от противного. В самом деле, если
такая последовательность из 26 различных букв существует, то
упомянутая разность равна сумме порядковых номеров букв алфавита. Однако
сумма
 при делении на 26 имеет остаток 13. Это доказывает утверждение
пункта б).
при делении на 26 имеет остаток 13. Это доказывает утверждение
пункта б).
Замечание. Утверждение пункта б) остается в силе для любого
алфавита из четного числа букв.
Представляет интерес доказательство пункта б), предложенноеучастниками олимпиады.
При делении на любое четное число суммы двух четных или двух нечетных чисел
получается четный остаток, а при делении суммы четного и нечетного
чисел - нечетный остаток.
Соответствующие буквы складываемых последовательностей могут быть как
одинаковой, так и различной четности. (Для краткости мы называем букву
четной, если ее номер четен, и нечетной - если номер нечетен.)
Будем решать задачу от противного. Предположим, что требуемая
последовательность существует. Всего в сложении участвуют 52 буквы. Пар
букв одинаковой и различной четности должно быть одинаковое количество,
а именно 13 (так как в результате сложения должно получиться 13 четных
и 13 нечетных букв). Пары букв различной четности включают в себя 26
букв. Оставшиеся 26 букв входят в 13 пар букв одинаковой четности.
Однако, 13 пар букв одинаковой четности не могут содержать одинаковое
количество четных и нечетных букв (так как 13 - нечетное число).
Полученное противоречие доказывает утверждение пункта б).
9.2.
В этой задаче условимся писать
 , если числа , если числа  и и  имеют одинаковые остатки
при делении на 33. Пусть имеют одинаковые остатки
при делении на 33. Пусть  - номер первой буквы искомой
последовательности. Эту букву указанное число раз прибавили к букве
К, в результате получили букву А. Запишем
соответствующее уравнение: - номер первой буквы искомой
последовательности. Эту букву указанное число раз прибавили к букве
К, в результате получили букву А. Запишем
соответствующее уравнение:
 |
(1) |
Имеем следующую цепочку соотношений:

Уравнение (1) принимает вид:
 ,
или ,
или
 |
(2) |
Пользуясь арифметикой остатков, несложно составить следующую
таблицу
| А |
Б |
В |
Г |
Д |
Е |
 |
Ж |
З |
И |
Й |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
Ф |
| 17 |
1 |
18 |
2 |
19 |
3 |
20 |
4 |
21 |
5 |
22 |
6 |
23 |
7 |
24 |
8 |
25 |
9 |
26 |
10 |
27 |
11 |
| |
| Х |
Ц |
Ч |
Ш |
Щ |
Ъ |
Ы |
Ь |
Э |
Ю |
Я |
|
| 28 |
12 |
29 |
13 |
30 |
14 |
31 |
15 |
32 |
16 |
0 |
|
Здесь под каждой буквой подписан остаток от деления на 33 результата
умножения ее номера на 17. Как видно из таблицы, уравнение (2)
имеет единственное решение  , т.е. первая буква
искомой последовательности - Й. Аналогично могут быть
найдены и остальные буквы. Искомая последовательность имеет вид , т.е. первая буква
искомой последовательности - Й. Аналогично могут быть
найдены и остальные буквы. Искомая последовательность имеет вид
 |
(3) |
Если последовательность (3) прибавить 17 раз к слову
КРИПТОША, то получится слово АНАЛИТИК. Ясно, что
если последовательность (3) прибавить к слову КРИПТОША
33 раза, то вновь получится КРИПТОША. Значит,
если (3) прибавить 16 раз к слову АНАЛИТИК, то
получится КРИПТОША. Получить слово КРИПТОША меньше
чем за 16 прибавлений не удастся. Действительно, рассмотрим
предпоследние буквы в этих словах и в последовательности (3):
Ш, И,
А.
Очевидно, что для получения буквы
Ш из буквы И необходимо
букву А прибавить к И по крайней мере 16 раз.
Ответ: ЙЩНЧЛЖАФ; 16 раз.
9.3.
В этой задаче условимся писать  , если числа , если числа
 и и  имеют одинаковые остатки при делении на 1000. Для нахождения
последней буквы исходного сообщения необходимо решить уравнение имеют одинаковые остатки при делении на 1000. Для нахождения
последней буквы исходного сообщения необходимо решить уравнение
 |
(1) |
Здесь  - пока неизвестное трехзначное число.
Пусть - пока неизвестное трехзначное число.
Пусть
 ( ( , ,  , ,  - цифры).
Тогда - цифры).
Тогда

Значит,  . Далее, . Далее,

Отсюда  . Тогда . Тогда

Значит,  и поэтому и поэтому  . .
Уравнение (1) могло быть решено иначе. Умножив обе части (1)
на 13, получим
 . Ясно, что последние три
цифры числа, стоящего в левой части равенства, совпадают с тремя
последними цифрами самого числа . Ясно, что последние три
цифры числа, стоящего в левой части равенства, совпадают с тремя
последними цифрами самого числа  . Вычислив . Вычислив
 ,
найдем ,
найдем  .
Теперь аналогично решаем уравнение (1), в правой части которого
стоят другие трехзначные цифровые группы шифрсообщения (850, 547, 550
и т.д.). .
Теперь аналогично решаем уравнение (1), в правой части которого
стоят другие трехзначные цифровые группы шифрсообщения (850, 547, 550
и т.д.).
Искомая цифровая последовательность имеет вид

Ответ: КЛЮЧШИФРАНАЙДЕН.
9.4. Сначала восстановим магический квадрат. Сумма чисел во всех клетках квадрата
равна
 , значит, в каждом столбце (а
также в строке, на диагонали) сумма чисел составляет , значит, в каждом столбце (а
также в строке, на диагонали) сумма чисел составляет
 . Попытаемся
построить магические квадраты с суммой на линии, равной 34,
и единицей в правом
нижнем углу. Имеется несколько таких квадратов.
Например, . Попытаемся
построить магические квадраты с суммой на линии, равной 34,
и единицей в правом
нижнем углу. Имеется несколько таких квадратов.
Например,
|
4 |
10 |
7 |
13 |
|
5 |
15 |
2 |
12 |
|
9 |
3 |
14 |
8 |
|
16 |
6 |
11 |
1 |
|
10 |
5 |
11 |
8 |
|
6 |
9 |
7 |
12 |
|
3 |
4 |
14 |
13 |
|
15 |
16 |
2 |
1 |
|
12 |
2 |
5 |
15 |
|
7 |
13 |
10 |
4 |
|
9 |
3 |
8 |
14 |
|
6 |
16 |
11 |
1 |
|
16 |
3 |
2 |
13 |
|
5 |
10 |
11 |
8 |
|
9 |
6 |
7 |
12 |
|
4 |
15 |
14 |
1 |
|
Расставляя буквы в соответствии с условием, только в одном случае,
отвечающем четвертому квадрату, получаем читаемый текст:
|
Ы |
Р |
Е |
У |
|
С |
Т |
Е |
В |
|
Ь |
Т |
А |
Б |
|
Е |
В |
К |
П |
|
П |
Е |
Р |
Е |
|
С |
Т |
А |
В |
|
Ь |
Т |
Е |
Б |
|
У |
К |
В |
Ы |
|
Ответ: 
9.5.
Пусть
 , ,
 , ,
 , ,
 радиус окружности
(см. рис. 25).
Условие (4) задачи эквивалентно равенству радиус окружности
(см. рис. 25).
Условие (4) задачи эквивалентно равенству

С учетом выражений
 и
и
 ,
это равенство можно записать в виде: ,
это равенство можно записать в виде:

Без ограничения общности
можно считать, что
 . Далее, поскольку координаты
точки . Далее, поскольку координаты
точки 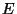 - целые числа, меньшие 5, могут иметь место три
случая. - целые числа, меньшие 5, могут иметь место три
случая.
Случай 1.  .
Равенство (1) примет вид: .
Равенство (1) примет вид:
 . Это
дает два варианта расположения точек: 1) . Это
дает два варианта расположения точек: 1)
 , ,  , ,  ; 2) ; 2)
 , ,  , ,  . .
Случай 2.
 .
Из (1) получаем: .
Из (1) получаем:
 .
Последнее равенство невозможно, так как правая часть равенства строго
меньше 6, а левая часть равенства
не меньше, чем .
Последнее равенство невозможно, так как правая часть равенства строго
меньше 6, а левая часть равенства
не меньше, чем
 . .
Случай 3.
 .
Равенство (1) запишется в виде: .
Равенство (1) запишется в виде:
 .
Это равенство невозможно,
так как .
Это равенство невозможно,
так как
 и
и
 . .
Ответ: 1)  , ,  , ,  ; 2) ; 2)  , ,
 , ,  . .
9.6.
Выделим под знаками радикала полный квадрат:

В результате замены
 неравенство примет вид:
неравенство примет вид:

Для решения последнего неравенства изучим взаимное расположение на плоскости
 полуокружностей полуокружностей

и

Точки пересечения полуокружностей (если этих точек две) расположены
симметрично относительно прямой, соединяющей их центры. В данном случае это
прямая  . Рассмотрим вначале качественно возможные взаимные
расположения полуокружностей. Если величина . Рассмотрим вначале качественно возможные взаимные
расположения полуокружностей. Если величина  мала, то
полуокружности не пересекаются (рис. 26). мала, то
полуокружности не пересекаются (рис. 26).
С ростом  у
полуокружностей появляется общая точка у
полуокружностей появляется общая точка  (с абсциссой (с абсциссой  )
(рис. 27).
При дальнейшем увеличении )
(рис. 27).
При дальнейшем увеличении  точка пересечения точка пересечения  ``движется'' по окружности
``движется'' по окружности  по
часовой стрелке. Значение по
часовой стрелке. Значение  , при котором точка , при котором точка  совпадает с
точкой совпадает с
точкой  , является критическим, так как при дальнейшем
увеличении , является критическим, так как при дальнейшем
увеличении  полуокружности имеют две точки пересечения (рис. 28). И,
наконец, при
полуокружности имеют две точки пересечения (рис. 28). И,
наконец, при  , превосходящем некоторое значение, полуокружности
вновь не пересекаются (рис. 29). Рассмотрим указанные случаи
подробно. , превосходящем некоторое значение, полуокружности
вновь не пересекаются (рис. 29). Рассмотрим указанные случаи
подробно.
Случай 1. При
 полуокружности не пересекаются, и неравенство
решений не имеет (рис. 26).
полуокружности не пересекаются, и неравенство
решений не имеет (рис. 26).
Случай 2.
Полуокружности имеют единственную точку пересечения
с абсциссой  (рис. 27).
При этом (рис. 27).
При этом
 . Решение
неравенства имеет вид . Решение
неравенства имеет вид ![$ t\in[-1;t_0]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1770.gif) . .
Случай 3. Полуокружности имеют две точки
пересечения (рис. 28). При этом
 . Решение неравенства
имеет вид . Решение неравенства
имеет вид
![$ t\hph\in[-1;t_1]\cup[t_2;3]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1772.gif) . При . При  имеет место
касание полуокружностей (можно считать, что точек пересечения
по-прежнему две, но просто они совпадают).
имеет место
касание полуокружностей (можно считать, что точек пересечения
по-прежнему две, но просто они совпадают).
Случай 4. При
 полуокружности вновь не имеют общих точек, и полуокружности вновь не имеют общих точек, и
![$ t\in[-1;3]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1775.gif) . .
Найдем теперь точные выражения для абсцисс  точек пересечения
окружностей. Эти величины удовлетворяют системе точек пересечения
окружностей. Эти величины удовлетворяют системе

Решая квадратное уравнение, находим

Итак, решение неравенства имеет вид:
1. 
 решений нет. решений нет.
2.

 ![$ t\in[-1;t_1]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1782.gif) . .
3.


![$ t\in[-1;t_1]\cup[t_2;3]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1783.gif) . .
4. 
 ![$ t\in[-1;3]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1775.gif) . .
Переходя к переменной 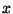 и используя явные выражения для и используя явные выражения для  ,
получаем окончательный ,
получаем окончательный
Ответ:
1. 
 решений нет. решений нет.
2.


![$ x\in[-\nfrac{3}{2};\nfrac{a^2-2-\sqrt{12\cdot a^2-a^4-4}}{4}]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1784.gif) . .
3.


![$ x\in[-\nfrac{3}{2};
\nfrac{a^2-2-\sqrt{12\cdot a^2-a^4-4}}{4}]\cup[
\nfrac{a^2-2+\sqrt{12\cdot a^2-a^4-4}}{4};\nfrac{5}{2}]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1785.gif) . .
4. 

![$ x\in[-\nfrac{3}{2};\nfrac{5}{2}]$](https://images.geo.web.ru/pubd/2001/10/08/0001161235/img1786.gif) . .
Next: Литература к главе 7
Up: 7.6. Указания и решения
Previous: ...к задачам восьмой олимпиады
Contents: Содержание
|

