




Вперед: 11.3.3 Логарифмирование в полях простого порядка
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.1 Алгоритм Гельфонда
Содержание
Предметный указатель
Этот алгоритм (см. также [PH], [Акр, упр. 24 к
разд. 3.3.1], [Odl], [Kob, гл. 4,
 3])
позволяет быстро вычислять дискретные логарифмы в группе 3])
позволяет быстро вычислять дискретные логарифмы в группе
 , если , если  гладкое,
т. е. все простые делители гладкое,
т. е. все простые делители  невелики. невелики.
Пусть
 , где , где 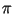 -- некоторое конечное множество простых чисел, а
-- некоторое конечное множество простых чисел, а
 . Предполагается, что множество . Предполагается, что множество 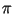 и числа
и числа  для каждого для каждого  известны (их можно
найти перебором). Алгоритм заключается в следующем:
1.
(Построение таблиц.) Для каждого известны (их можно
найти перебором). Алгоритм заключается в следующем:
1.
(Построение таблиц.) Для каждого  вычислим
набор элементов вычислим
набор элементов
 , ,
 . Отметим, что порядок . Отметим, что порядок
 равен
равен  , поэтому , поэтому
 |
(1) |
-- все попарно различные корни  -й степени из единицы в
группе -й степени из единицы в
группе  . Набор (1) называется
таблицей корней . Набор (1) называется
таблицей корней  -й степени из единицы. -й степени из единицы.
2.
(Вычисление
 для для
 .) Обозначим через .) Обозначим через  искомый (пока неизвестный) искомый (пока неизвестный)
 -- дискретный логарифм -- дискретный логарифм  по основанию по основанию  . Для
каждого . Для
каждого  пусть пусть
 ,
где ,
где
 . Будем последовательно
искать . Будем последовательно
искать
 следующим способом: следующим способом:
2.1.
Вычислим
 . Так как . Так как  , где , где
 , мы получаем, что , мы получаем, что
 Поэтому для вычисления
Поэтому для вычисления  достаточно сравнить достаточно сравнить
 с элементами таблицы (1) и положить с элементами таблицы (1) и положить
 равным тому равным тому  , для которого , для которого
 . .
2.2.
Пусть
 уже найдены. Вычислим уже найдены. Вычислим
 Так как
Так как  , где , где
 , мы
получаем, что , мы
получаем, что
 Поэтому для вычисления
Поэтому для вычисления  достаточно сравнить элемент достаточно сравнить элемент
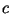 с элементами таблицы (1) и положить с элементами таблицы (1) и положить  равным тому
равным тому  , для которого , для которого  . .
Таким образом, мы находим
 и, следовательно, и, следовательно,
 для всех
для всех  . .
3.
(Вычисление  .) Используя китайскую теорему
об остатках, вычислим искомый дискретный логарифм .) Используя китайскую теорему
об остатках, вычислим искомый дискретный логарифм
 по по
 для для  ,
найденным на этапе 2 (см., например,
[Акр, разд. 2.3.2]). ,
найденным на этапе 2 (см., например,
[Акр, разд. 2.3.2]).
Отметим, что если все  не превосходят некоторого
полинома от не превосходят некоторого
полинома от  , то вышеописанный алгоритм
полиномиален от , то вышеописанный алгоритм
полиномиален от  . .





Вперед: 11.3.3 Логарифмирование в полях простого порядка
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.1 Алгоритм Гельфонда
Содержание
Предметный указатель
|

