




Вперед: 11.3.4 Алгоритм Хеллмана - Рейнери
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.2 Алгоритм Полига - Хеллмана
Содержание
Предметный указатель
В этом подразделе мы считаем, что  , т. e. будем
рассматривать дискретное логарифмирование в группе , т. e. будем
рассматривать дискретное логарифмирование в группе
 , где , где  -- простое число. Для удобства мы будем
работать с полем вычетов -- простое число. Для удобства мы будем
работать с полем вычетов
 по модулю по модулю  и с его
мультипликативной группой и с его
мультипликативной группой
 . .
В работе Коямы [Koy] приведены результаты о
логарифмировании в
 , которые означают следующее:
1.
Сложность решения уравнения , которые означают следующее:
1.
Сложность решения уравнения  , где , где
 , не зависит от , не зависит от  и и  . .
2.
Решить систему уравнений
 не легче, чем одно уравнение
не легче, чем одно уравнение  (
(
 ). ).
Положим
 . Следующий
алгоритм приводится в виде схемы, не претендующей на
подробное описание: . Следующий
алгоритм приводится в виде схемы, не претендующей на
подробное описание:
1.
Разложить 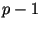 на простые множители (с помощью
одного из алгоритмов факторизации целых чисел): на простые множители (с помощью
одного из алгоритмов факторизации целых чисел):
 , где , где  --
конечное множество простых чисел, а --
конечное множество простых чисел, а
 . .
2.
Выбрать границу гладкости
![$ L_{1}=[L(p)^{c}]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1325.gif) (где (где
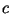 -- некоторая константа) и найти множество -- некоторая константа) и найти множество 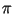 всех
простых чисел, не превосходящих всех
простых чисел, не превосходящих  (множество (множество 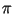 называется факторной базой).
называется факторной базой).
3.
Случайно перебирая целые числа 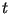 , ,
 , выбрать те, для которых либо , выбрать те, для которых либо
 ,
либо ,
либо
 является гладким по отношению к границе
гладкости является гладким по отношению к границе
гладкости  , т. е. , т. е.
4.
Пусть на предыдущем этапе найдены
 гладких чисел гладких чисел
 , ,
 , и , и  гладких чисел
гладких чисел
 , ,
 . Построить
векторы показателей . Построить
векторы показателей
Отметим, что если через
 обозначить
вектор обозначить
вектор
 , то, логарифмируя
соотношения (2) и (3), можно получить,
что , то, логарифмируя
соотношения (2) и (3), можно получить,
что
где
 обозначает скалярное произведение по
модулю обозначает скалярное произведение по
модулю 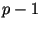 : :

5.
Для каждого  выразить один из векторов выразить один из векторов
 через векторы через векторы
 . Для того, чтобы это было
возможно, . Для того, чтобы это было
возможно,  должно быть достаточно велико. должно быть достаточно велико.
6.
Пусть на предыдущем этапе найдено соотношение
 , где , где
 . Тогда из (4)
и (5) следует, что . Тогда из (4)
и (5) следует, что
 и, следовательно, мы можем найти
и, следовательно, мы можем найти
 . .
7.
Вычислив
 для
всех для
всех  , с помощью китайской теоремы об
остатках найти , с помощью китайской теоремы об
остатках найти
 . .
Приведенный алгоритм описан в работе Адлемана [Adl],
но основные идеи этого алгоритма были изложены в работе
Вестерна и Миллера [WM] в 1968 г. В [Adl]
получена эвристическая оценка
 его
сложности при условии использования одного из
субэкспоненциальных алгоритмов для факторизации его
сложности при условии использования одного из
субэкспоненциальных алгоритмов для факторизации 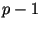 . В
этой работе рассмотрен и случай, когда . В
этой работе рассмотрен и случай, когда  не является
порождающим не является
порождающим
 , т. е. логарифмирование производится
в подгруппе группы , т. е. логарифмирование производится
в подгруппе группы
 . Также замечено, что этот
общий случай можно свести к случаю, когда . Также замечено, что этот
общий случай можно свести к случаю, когда  является
порождающим является
порождающим
 . .
Заметим, что, вообще говоря, факторизация 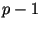 не является
необходимой. Достаточно найти один гладкий элемент не является
необходимой. Достаточно найти один гладкий элемент
 и пытаться выразить его через произведение
степеней гладких элементов и пытаться выразить его через произведение
степеней гладких элементов
 , т. е. проводить исключение в показателях сразу по модулю , т. е. проводить исключение в показателях сразу по модулю 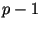 . .
На этапе 5 алгоритма приходится решать разреженные системы
линейных уравнений в кольцах вычетов
 . В ряде работ
(см. [Copp], [COS]) указано, что метод гауссова
исключения здесь не является оптимальным. Предлагается
использовать, например, алгоритмы Ланцоша [Lanc] или
Видемана [Wied] (см. об этом [COS]). В работе
[Gord] описан новый метод исключения, предложенный
Померансом. . В ряде работ
(см. [Copp], [COS]) указано, что метод гауссова
исключения здесь не является оптимальным. Предлагается
использовать, например, алгоритмы Ланцоша [Lanc] или
Видемана [Wied] (см. об этом [COS]). В работе
[Gord] описан новый метод исключения, предложенный
Померансом.
Дальнейшее развитие указанного метода логарифмирования в
 получено Копперсмитом, Одлыжко и Шреппелем в
работе [COS]. Сложность вычисления дискретного
логарифма доведена до получено Копперсмитом, Одлыжко и Шреппелем в
работе [COS]. Сложность вычисления дискретного
логарифма доведена до
 . Согласно
[McC90, стр. 66], алгоритм [COS] был реализован
на ЭВМ; результат (см. [LaMO]) позволяет
предположить, что вычисление логарифма в . Согласно
[McC90, стр. 66], алгоритм [COS] был реализован
на ЭВМ; результат (см. [LaMO]) позволяет
предположить, что вычисление логарифма в
 на ЭВМ
можно проводить за реальное время при на ЭВМ
можно проводить за реальное время при  порядка порядка
 . .





Вперед: 11.3.4 Алгоритм Хеллмана - Рейнери
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.2 Алгоритм Полига - Хеллмана
Содержание
Предметный указатель
|

