




Вперед: 11.3.5 Алгоритм Копперсмита
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.3 Логарифмирование в полях простого порядка
Содержание
Предметный указатель
Рассмотрим теперь случай, когда  невелико. Тогда для
дискретного логарифмирования в невелико. Тогда для
дискретного логарифмирования в  применим следующий
алгоритм (см. [HR], [Kob, гл. 4, применим следующий
алгоритм (см. [HR], [Kob, гл. 4,
 3]). 3]).
1.
Поле  представим в виде факторкольца представим в виде факторкольца
![$ GF(p)[y]/(f(y))$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1368.gif) , где , где  -- неприводимый
многочлен степени -- неприводимый
многочлен степени  . Поэтому можно считать, что элементы . Поэтому можно считать, что элементы
 есть многочлены из есть многочлены из ![$ GF(p)[y]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1370.gif) степени не выше степени не выше
 . Элемент . Элемент
 имеет порядок имеет порядок 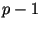 ,
следовательно, он является порождающим ,
следовательно, он является порождающим  . Зная
его, составляем таблицу логарифмов "констант" --
элементов . Зная
его, составляем таблицу логарифмов "констант" --
элементов  (логарифмы по основанию (логарифмы по основанию  ). Так как ). Так как
 невелико, то это можно сделать эффективно. невелико, то это можно сделать эффективно.
2.
Пусть  -- множество всех неприводимых
многочленов из -- множество всех неприводимых
многочленов из ![$ GF(p)[y]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1370.gif) степени не выше степени не выше  , где , где  --
некоторое натуральное число, меньшее --
некоторое натуральное число, меньшее  . .
3.
Случайно перебирая 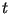 , ,
 ,
находим те из них, для которых ,
находим те из них, для которых
 где
где
 и и
 . (Разложение . (Разложение
 на множители можно находить, например, с
помощью алгоритма Берлекэмпа (см. [Акр, разд. 6.2.4]), эффективного при малых на множители можно находить, например, с
помощью алгоритма Берлекэмпа (см. [Акр, разд. 6.2.4]), эффективного при малых  ). Им
соответствуют уравнения ). Им
соответствуют уравнения
 относительно неизвестных
относительно неизвестных  . .
4.
Получив на предыдущем этапе достаточно много
уравнений относительно  , ,  , решаем систему
уравнений и находим , решаем систему
уравнений и находим  , ,  . .
5.
Находим 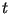 , такое, что , такое, что
 где
где
 и и
 . Тогда искомый
дискретный логарифм равен . Тогда искомый
дискретный логарифм равен
 Этот алгоритм имеет субэкспоненциальную сложность.
Этот алгоритм имеет субэкспоненциальную сложность.
Несколько иную схему логарифмирования в  предложил
Эль Гамаль [ElG84], [ElG85], [ElG86]. Оценка
сложности алгоритмов Эль Гамаля субэкспоненциальная (при
некоторых эвристических допущениях). предложил
Эль Гамаль [ElG84], [ElG85], [ElG86]. Оценка
сложности алгоритмов Эль Гамаля субэкспоненциальная (при
некоторых эвристических допущениях).





Вперед: 11.3.5 Алгоритм Копперсмита
Вверх: 11.3 Логарифмирование в GF(q)*
Назад: 11.3.3 Логарифмирование в полях простого порядка
Содержание
Предметный указатель
|

