13.2 Вероятностные тесты на простоту

Далее мы будем находить большие простые числа, перебирая натуральные числа из некоторых множеств. Нам необходимо быстро обнаруживать и отбрасывать числа, являющиеся составными, и оставлять для дальнейшего строгого доказательства простоты числа, которые скорее всего (с высокой вероятностью) действительно будут простыми. Этой цели служат вероятностные тесты на простоту. Такие тесты либо определяют, что составное, либо не дают определенного ответа о простоте . Однако во втором случае будет простым с высокой вероятностью. Вероятностные тесты быстро отсеивают составные числа, однако доказать с их помощью простоту числа нельзя.

Рассмотрим алгоритм Миллера -- Рабина [Rab]. Именно он обычно используется при построении больших простых чисел. Алгоритм основан на следующей теореме.

Пусть  -- нечетное составное число. Рассмотрим множество натуральных чисел , , для которых выполнено одно из следующих условий:

;

    2) при некотором таком, что , выполнены неравенства

Тогда количество элементов в не меньше .

Алгоритм Миллера -- Рабина заключается в случайном переборе значений , , и проверке для них условий 1) и 2). Если хотя бы одно из них выполнено, то  -- составное число. Если же эти условия не выполнены для случайных значений , то можно считать, что  -- простое с вероятностью не менее .

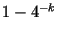Имеются и другие работы, посвященные вероятностным тестам на простоту (см. [SStr], [BBCGP], [Mon], [Boyd1], [DiPFM], [AS], [JU]). Однако для практических целей тест Миллера -- Рабина вполне эффективен и достаточен.

В работе [BBCGP] обсуждается вопрос, насколько соответствует действительности утверждение "вероятно простое" для числа , успешно прошедшего тест Миллера -- Рабина раз? Ответ таков: мы верим, что простое, поскольку иначе мы наблюдали чрезвычайно редкое событие вероятности не более . Однако здесь возникает другой вопрос о случайности выбираемых в тесте значений и о том, как распределены на отрезке натурального ряда те числа , для которых тест не выполняется (в случае составного ).