13.1 Введение

Большие простые числа, часто с дополнительными свойствами, используются практически во всех системах асимметричного шифрования, схемах генерации ключей и электронной подписи. Стойкость этих схем существенно зависит от некоторых тонких свойств используемых простых чисел. Таким образом, задача построения "типичного" простого числа имеет большое практическое значение.

Пусть нам нужно получить простое число с определенным количеством знаков в десятичной записи. Для этого мы можем просто выбрать случайное натуральное число из отрезка ; из асимптотического закона распределения простых чисел следует, что при достаточно больших выбранное число будет простым с вероятностью не менее , где 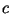 -- некоторая положительная константа. Но тогда возникает вопрос: как определить, действительно ли число простое? Возможны следующие подходы к решению этой задачи.

1. Проверим, делится ли на маленькие простые числа до некоторой границы. Здесь мы отбросим составные числа с маленькими простыми делителями. Если мы хотим этим способом доказать простоту , то надо перебрать все .

2. Если  -- простое число, то для него справедлива малая теорема Ферма: если , то , или для всех целых . Поэтому если для некоторого малая теорема Ферма не выполнена, то  -- составное число. Это эффективный тест для отбрасывания практически всех составных чисел. Например, первые 10 нечетных чисел вида , , прошедших тест , действительно оказались простыми. (Как обычно, запись здесь и далее обозначает наибольший общий делитель чисел и .)

Однако если прошло через тесты вида при или для нескольких значений , то это еще не означает, что оно простое. Существуют нечетные составные числа , называемые числами Кармайкла, такие, что для всех целых чисел и для всех целых , взаимно простых с . Недавно доказано [AGP], что чисел Кармайкла бесконечно много.

3. Проверим теперь на строгую псевдопростоту. Пусть  -- нечетное число такое, что , где нечетно, . Число называется строго псевдопростым в базе , , если , и либо , либо при некотором , . Как показано в [AS], среди нечетных чисел , удовлетворяющих неравенству и строго псевдопростых в базах 2, 3, 5, 7, составным является только одно число ; все остальные являются простыми числами. Если же число не является строго псевдопростым в некоторой базе , то  -- составное число (это следует из малой теоремы Ферма).

Тест, аналогичный тесту строгой псевдопростоты, присутствует в следующем алгоритме Миллера [Mil]. В нем  -- нечетное число, , где нечетно.     1. Проверить, является ли -й степенью натурального числа при каком-либо . Если да, то составное.

    2. Для всех , , где  -- некоторая функция от , проверить следующие условия:

  2.1. ;

  2.2. ;

  2.3. при некотором , .

Если какое-либо из условий 2.1-2.3 истинно, то составное.

Если мы положим и данный алгоритм не обнаружит, что составное число, то является простым, и алгоритм будет детерминированно проверять простоту за арифметических операций.

Если справедлива расширенная гипотеза Римана, то можно положить , и алгоритм Миллера будет проверять простоту за операций. Однако к настоящему времени расширенная гипотеза Римана не доказана.

4. При применении предыдущих подходов мы либо отбрасывали составные числа, либо детерминированно проверяли простоту числа с экспоненциальной сложностью. В 1980-1984 годах Адлеман, Ленстра и Коэн предложили ряд алгоритмов, которые позволяют детерминированно проверять простоту за операций. Обзор этих и предшествовавших им алгоритмов см. в [Вас1]. Применение этих методов позволяет проверить простоту натурального числа порядка за несколько минут (в зависимости от быстродействия компьютера). Однако если нам нужны простые числа с тысячами десятичных знаков, то эти алгоритмы становятся непригодными.

Среди последних достижений в области построения общих алгоритмов проверки простоты отметим алгоритм Гольдвассер -- Килиана [GKil], который работает с полиномиальной сложностью для от всех чисел, имеющих длину десятичной записи не более .

Важный результат получен в работах Адлемана и Хуанга [AHu1], [AHu2]. В их алгоритме для случайно выбранного , , проверяется выполнение некоторых условий, из которых следует простота , причем если -- простое число, то вероятность выбрать то , для которого условия будут выполнены, не менее .

В разделах 13.3-13.6 мы приводим различные методы тестирования простоты и построения больших простых чисел. По-видимому, наиболее надежным и проверенным на практике является метод, основанный на теореме Бриллхарта, Лемера и Селфриджа и описанный в разделе 13.5. Мы рекомендуем его для использования в сочетании с методом Конягина -- Померанса, описанным в в разделе 13.6. Раздел 13.7 посвящен анализу алгоритма построения больших простых чисел, используемого в отечественном стандарте электронной подписи (ГОСТ Р 34.10-94). В частности, указаны его недостатки и способы их преодоления. Наконец, в разделе 13.8 предлагается некоторая модификация алгоритма из отечественного стандарта электронной подписи, учитывающая замечания, высказанные в разделе 13.7.