




Вперед: 13.7.1 Общетеоретические обоснования
Вверх: 13. Методы построения больших простых чисел
Назад: 13.6 Полиномиальные алгоритмы доказательства простоты n с помощью известного полного разложения n-1 на простые множители
Содержание
Предметный указатель
13.7 Анализ алгоритма построения
больших простых чисел, изложенного в Стандарте
(ГОСТ Р 34.10-94) "Процедуры выработки и проверки
электронной цифровой подписи на базе асимметричного
криптографического алгоритма"
В указанном Стандарте предлагается алгоритм построения
простых чисел  длины длины 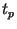 битов, битов,
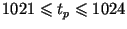 , с простым делителем , с простым делителем  длины длины 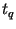 битов,
битов,
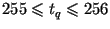 , числа , числа 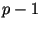 . При
этом частное . При
этом частное 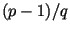 также имеет большой простой делитель также имеет большой простой делитель
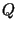 длины 512 битов. Наличие достаточно больших простых
делителей у числа длины 512 битов. Наличие достаточно больших простых
делителей у числа 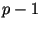 вызвано требованиями предлагаемого
Стандартом алгоритма электронной цифровой подписи. Алгоритм
построения чисел вызвано требованиями предлагаемого
Стандартом алгоритма электронной цифровой подписи. Алгоритм
построения чисел  с указанными свойствами предлагается в
двух модификациях (Процедуры В и В с указанными свойствами предлагается в
двух модификациях (Процедуры В и В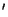 ), ориентированных
соответственно на 16- и 32-битовые вычислительные машины.
Модификации отличаются лишь размерами случайных чисел,
вырабатываемых случайными датчиками, основанными на
линейном конгруэнтном методе и указанными в Стандарте. В
Процедуре В такой датчик имеет вид ), ориентированных
соответственно на 16- и 32-битовые вычислительные машины.
Модификации отличаются лишь размерами случайных чисел,
вырабатываемых случайными датчиками, основанными на
линейном конгруэнтном методе и указанными в Стандарте. В
Процедуре В такой датчик имеет вид
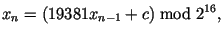 а в процедуре В
а в процедуре В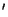
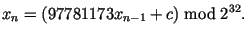 Основу указанных процедур составляют соответственно
Процедуры А и А
Основу указанных процедур составляют соответственно
Процедуры А и А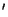 , позволяющие строить при каждом целом , позволяющие строить при каждом целом
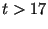 простые числа простые числа  длины длины 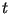 битов с простым делителем битов с простым делителем
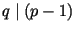 длины длины ![$ [t/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1769.gif) битов (здесь битов (здесь ![$ [\,.\,]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1770.gif) -- целая
часть числа). Процедуры А и А -- целая
часть числа). Процедуры А и А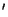 также отличаются лишь
размерами используемых случайных чисел. Мы опишем в
п. 13.7.2 и затем проанализируем алгоритм, лежащий в
основе этих процедур, на примере процедуры А. Использование
этого алгоритма в процедурах В и В также отличаются лишь
размерами используемых случайных чисел. Мы опишем в
п. 13.7.2 и затем проанализируем алгоритм, лежащий в
основе этих процедур, на примере процедуры А. Использование
этого алгоритма в процедурах В и В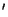 не имеет
принципиальных отличий. не имеет
принципиальных отличий.





Вперед: 13.7.1 Общетеоретические обоснования
Вверх: 13. Методы построения больших простых чисел
Назад: 13.6 Полиномиальные алгоритмы доказательства простоты n с помощью известного полного разложения n-1 на простые множители
Содержание
Предметный указатель
|

