




Вперед: 13.7.6 Замечания
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.4 Распознает ли Алгоритм все простые числа?
Содержание
Предметный указатель
Можно добиться существенного сокращения времени работы
Алгоритма, если предусмотреть в нем специальные приемы
обработки составных чисел.
Составные числа вида 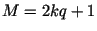 отсеиваются в Алгоритме
с помощью теста теоремы 8. Но
для большинства из них непростоту можно доказать
значительно быстрее. Так каждое третье число в прогрессии
делится на 3, каждое пятое делится на 5 и т. д. Пользуясь
регулярностью расположения этих чисел, их можно вообще не
рассматривать, перескакивая через них при выборе
нового значения u в шаге 8 Алгоритма. Это просеивание
можно проделать следующим способом. отсеиваются в Алгоритме
с помощью теста теоремы 8. Но
для большинства из них непростоту можно доказать
значительно быстрее. Так каждое третье число в прогрессии
делится на 3, каждое пятое делится на 5 и т. д. Пользуясь
регулярностью расположения этих чисел, их можно вообще не
рассматривать, перескакивая через них при выборе
нового значения u в шаге 8 Алгоритма. Это просеивание
можно проделать следующим способом.
Определив в пункте 4 Алгоритма очередное четное число
 , составим таблицу всех чисел , составим таблицу всех чисел  из промежутка из промежутка
 с условием, что с условием, что  и 15
взаимно просты. Это очень просто сделать, заставив и 15
взаимно просты. Это очень просто сделать, заставив  пробегать все числа
пробегать все числа
 и вычисляя наибольший
общий делитель 15 и и вычисляя наибольший
общий делитель 15 и  . Вычисления можно еще
упростить, если предварительно вычислить остатки от
деления на 15 чисел . Вычисления можно еще
упростить, если предварительно вычислить остатки от
деления на 15 чисел  и и  . Эта таблица чисел . Эта таблица чисел  будет
состоять из 8 чисел будет
состоять из 8 чисел
 . Положим также . Положим также
 Вместо одной переменной
Вместо одной переменной 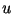 в Алгоритме нужно
рассматривать две переменные в Алгоритме нужно
рассматривать две переменные 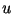 и и  , положив в шаге 5 , положив в шаге 5
 , ,
 , а затем вычисляя в шаге 8 , а затем вычисляя в шаге 8
 Легко видеть, что все числа прогрессии
Легко видеть, что все числа прогрессии  , ,
 , делящиеся на 3 или 5, будут при этом
пропущены. , делящиеся на 3 или 5, будут при этом
пропущены.
Можно расширить количество маленьких делителей, добавив
к множеству  число число  и т. д. При этом
доля остающихся в результате просеивания чисел будет равна
соответственно и т. д. При этом
доля остающихся в результате просеивания чисел будет равна
соответственно
 и т. д.
Отметим, что длина таблицы остатков будет при этом равна и т. д.
Отметим, что длина таблицы остатков будет при этом равна
 , т. е. будет довольно быстро
увеличиваться. , т. е. будет довольно быстро
увеличиваться.
Иной вариант организации просеивания, не использующий много
памяти, но требующий несколько большего объема
вычислений, можно реализовать так. Будем использовать
вместо одной переменной  две переменные две переменные  и и  ,
которые будут равны остаткам от деления числа ,
которые будут равны остаткам от деления числа  на 3 и 5 соответственно. Для этого шаг 5 представим как
три следующих шага:
5.1.
Положить
на 3 и 5 соответственно. Для этого шаг 5 представим как
три следующих шага:
5.1.
Положить

5.2.
Если  и и  , перейти в пункт 6. , перейти в пункт 6.
5.3.
Положить
 и перейти в шаг 5.2.
и перейти в шаг 5.2.
Кроме того, приведенный выше пункт 8.5 Алгоритма нужно
изменить следующим образом:
8.5.
Перейти в пункт 5.3.
Как и выше, можно увеличить множество простых делителей
 , добавив к ним числа , добавив к ним числа  и т. д. и т. д.
Описанные выше приемы просеивания, исключают из рассмотрения
числа
 , имеющие маленькие простые
делители. В качестве еще одного средства отсеивания
составных чисел , имеющие маленькие простые
делители. В качестве еще одного средства отсеивания
составных чисел  можно использовать следующие
изменения в пункте 7:
7.
Если можно использовать следующие
изменения в пункте 7:
7.
Если
 , то перейти к шагу 4. В
противном случае проверить делимость числа , то перейти к шагу 4. В
противном случае проверить делимость числа  на все
простые числа, не превосходящие некоторой границы на все
простые числа, не превосходящие некоторой границы  .
В случае делимости вычислить новое значение .
В случае делимости вычислить новое значение 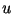 (перейти в
пункт 5.3). (перейти в
пункт 5.3).
Для реализации этого пункта нужно предварительно, скажем,
в пункте 1 Алгоритма запасти таблицу всех простых
чисел, не превосходящих  . .
После указанных в этом параграфе изменений к тестам
пункта 8 будут приходить только числа
 , все простые делители которых
превосходят границу , все простые делители которых
превосходят границу  . .





Вперед: 13.7.6 Замечания
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.4 Распознает ли Алгоритм все простые числа?
Содержание
Предметный указатель
|

