




Вперед: 13.7.3 Всегда ли результатом работы Алгоритма являются простые числа?
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.1 Общетеоретические обоснования
Содержание
Предметный указатель
13.7.2 Алгоритм
В основу используемого в Стандарте алгоритма
построения больших простых чисел  положена следующая
теорема (отметим, что в Стандарте отсутствуют ссылки
на какую-нибудь научную литературу, что создает
определенные трудности при анализе). положена следующая
теорема (отметим, что в Стандарте отсутствуют ссылки
на какую-нибудь научную литературу, что создает
определенные трудности при анализе).
Теорема 8.
Пусть 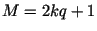 , ,
 , где , где
 -- нечетное простое число, -- нечетное простое число,  -- натуральное число,
взаимно простое с -- натуральное число,
взаимно простое с  , и , и
Тогда, если
 то то  -- простое число. -- простое число.
В Алгоритме эта теорема используется при 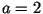 . .
Алгоритм строит последовательность простых чисел
 длины
длины
 соответственно, причем соответственно, причем
![$ t_{i+1}=[t_i/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1798.gif) , ,
 , ,  . При этом
построение начинается с . При этом
построение начинается с  и для и для
 число
число  строится по строится по  в виде в виде
 и число
и число  всякий раз подбирается так, чтобы при всякий раз подбирается так, чтобы при 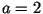 были выполнены условия теоремы 8. Простые числа
были выполнены условия теоремы 8. Простые числа
 и и  имеют все необходимые свойства. Дадим
теперь формальное описание Алгоритма. При этом мы
опускаем построение последовательности случайных чисел имеют все необходимые свойства. Дадим
теперь формальное описание Алгоритма. При этом мы
опускаем построение последовательности случайных чисел
 , равномерно распределенной на интервале , равномерно распределенной на интервале  . Для
наших целей это построение не принципиально. . Для
наших целей это построение не принципиально.
Алгоритм построения простых чисел  и и
 , ,
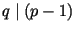 ,
имеющих длину соответственно ,
имеющих длину соответственно 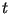 и и ![$ [t/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1769.gif) битов:
1.
Вычислить последовательность чисел битов:
1.
Вычислить последовательность чисел
 по правилу: по правилу:
 ; ;
если
 , то , то
![$ t_{i+1}=[t_i/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1798.gif) ; ;
если  , то , то  . .
2.
Найти наименьшее простое число  длины длины
 битов. битов.
3.
 . .
4.
Вычислить случайное число  на интервале на интервале
 и положить и положить
![$\displaystyle N=\left\lceil2^{t_m-1}/p_{m+1}\right\rceil+
\left[\left(2^{t_m-1}\cdot\xi\right)/p_{m+1}\right].
$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1816.gif) (Здесь
(Здесь ![$ [x]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1817.gif) и и
 обозначают целую часть числа обозначают целую часть числа
 и наименьшее целое, не меньшее, чем и наименьшее целое, не меньшее, чем  .) Если .) Если  нечетно, положить
нечетно, положить
 . .
5.
 . .
6.
Вычислить
 . .
7.
Если
 , то перейти к шагу 4. , то перейти к шагу 4.
8.
Проверить условия
Если хотя бы одно из условий не выполнено, то положить
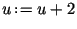 , и перейти к шагу 6. Если выполнены оба
условия, то положить , и перейти к шагу 6. Если выполнены оба
условия, то положить
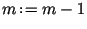 . .
9.
Если
 , то перейти к шагу 4. Если же , то перейти к шагу 4. Если же
 , то , то  и и  -- искомые простые числа. -- искомые простые числа.





Вперед: 13.7.3 Всегда ли результатом работы Алгоритма являются простые числа?
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.1 Общетеоретические обоснования
Содержание
Предметный указатель
|

