




Вперед: 13.7.4 Распознает ли Алгоритм все простые числа?
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.2 Алгоритм
Содержание
Предметный указатель
Указанный алгоритм, вообще говоря, может выдавать в
качестве  и и  составные числа. составные числа.
Выбор  , указанный в пункте 4, и пункт 7
Алгоритма обеспечивают выполнение неравенств , указанный в пункте 4, и пункт 7
Алгоритма обеспечивают выполнение неравенств
 |
(4) |
означающих в силу нечетности  , что длина , что длина  в
точности равняется в
точности равняется  битов. Кроме того, если битов. Кроме того, если  четно,
то четно,
то
 и из (4) следует и из (4) следует
 т. е. выполнены условия первого пункта теоремы 8
и можно утверждать, что
т. е. выполнены условия первого пункта теоремы 8
и можно утверждать, что  -- простое число. -- простое число.
Если же  нечетно, то нечетно, то
 и и
 При
При  , близком к своему наименьшему возможному
значению , близком к своему наименьшему возможному
значению
 , возможные для , возможные для  значения,
близкие к значения,
близкие к
 , будут примерно равны , будут примерно равны
 , т. е. , т. е.  . Это означает, что
параметры будут находиться вне пределов справедливости
теоремы 8 и, следовательно, гарантировать простоту числа . Это означает, что
параметры будут находиться вне пределов справедливости
теоремы 8 и, следовательно, гарантировать простоту числа
 в таком случае нельзя. в таком случае нельзя.
Если исходное значение  , скажем, 256 или 512, то все
числа , скажем, 256 или 512, то все
числа  четны и все четны и все  на основании
теоремы 8 просты. Но, если, например, на основании
теоремы 8 просты. Но, если, например,  , все
числа , все
числа  нечетны и тогда на каждом шаге Алгоритма нельзя
гарантировать простоту нечетны и тогда на каждом шаге Алгоритма нельзя
гарантировать простоту  и, следовательно, простоту и, следовательно, простоту
 и и  . Но именно 255 указывается в процедуре В
как допустимое значение длины числа . Но именно 255 указывается в процедуре В
как допустимое значение длины числа  , используемого в
алгоритме цифровой подписи. , используемого в
алгоритме цифровой подписи.
Указанную неточность в Алгоритме можно исправить
несколькими способами.
а) Можно было бы определить последовательность
 в шаге 1 Алгоритма равенствами в шаге 1 Алгоритма равенствами
![$ t_{i+1}=[(t_i+1)/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1846.gif) . Тогда при любом . Тогда при любом  выполняется
неравенство выполняется
неравенство
 и из (4) следует и из (4) следует
 Это в силу теоремы 8 позволяет утверждать, что
Это в силу теоремы 8 позволяет утверждать, что
 -- простое число. При этом битовая длина числа -- простое число. При этом битовая длина числа  ,
получаемого в результате работы Алгоритма, будет равна ,
получаемого в результате работы Алгоритма, будет равна
![$ [(t+1)/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1849.gif) . При нечетных . При нечетных 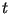 оно будет длиннее на 1 бит. оно будет длиннее на 1 бит.
Если 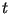 равно равно  , такое изменение Алгоритма не
приведет к увеличению числа итераций. Не изменится число
итераций и для , такое изменение Алгоритма не
приведет к увеличению числа итераций. Не изменится число
итераций и для  . А вот для . А вот для  изменение
Алгоритма приведет к увеличению числа итераций на 1. изменение
Алгоритма приведет к увеличению числа итераций на 1.
б) Увеличение диапазона для  в
теореме 8 позволяет при заданном в
теореме 8 позволяет при заданном  строить
простые числа, имеющие большую величину. Однако условие строить
простые числа, имеющие большую величину. Однако условие
 в формулировке теоремы ослабить нельзя.
Так, возможен случай, когда для составного в формулировке теоремы ослабить нельзя.
Так, возможен случай, когда для составного
 выполнены условия (2)
и (3).
Например, этот случай имеет место
1)
при выполнены условия (2)
и (3).
Например, этот случай имеет место
1)
при  , ,  , ,  ; ;
2)
при  , ,  , ,  ; ;
3)
при  , ,  , ,  ; ;
4)
при  , ,  , ,  ; ;
5)
при  , ,  , ,  . .
В следующей теореме описываются исключительные случаи,
которые могут возникать при увеличении интервала возможных
значений  до до  . .
Теорема 9.
Пусть 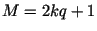 , ,
 , где , где
 -- нечетное простое число, -- нечетное простое число,  -- натуральное число,
взаимно простое с -- натуральное число,
взаимно простое с  , и , и
Тогда если
 , то , то  -- простое число или -- простое число или
 , где , где  -- простое число. В последнем
случае также выполняется сравнение -- простое число. В последнем
случае также выполняется сравнение
 |
(5) |
Следствие.
Если выполнены условия теоремы 9 и
 , ,
 , то , то  -- простое число. -- простое число.
Нам не известны простые числа  , удовлетворяющие
одновременно двум условиям , удовлетворяющие
одновременно двум условиям
Среди простых чисел
 имеется лишь два
числа 1093 и 3511, удовлетворяющих условию (6).
Условие (7) для них, конечно же,
нарушается. Тем не менее мы не должны исключать возможность
составного числа имеется лишь два
числа 1093 и 3511, удовлетворяющих условию (6).
Условие (7) для них, конечно же,
нарушается. Тем не менее мы не должны исключать возможность
составного числа  при при
 , хотя
эта возможность и маловероятна. , хотя
эта возможность и маловероятна.
Изменим пункт 8 Алгоритма, добавив в него проверку
условия
 . .
Так как при любом  справедливо неравенство справедливо неравенство
 , то при выполнении условий
пункта 8 Алгоритма будем иметь , то при выполнении условий
пункта 8 Алгоритма будем иметь
 Это означает выполнимость всех условий следствия из
теоремы 9. Но тогда можно утверждать простоту
числа
Это означает выполнимость всех условий следствия из
теоремы 9. Но тогда можно утверждать простоту
числа  . .





Вперед: 13.7.4 Распознает ли Алгоритм все простые числа?
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.2 Алгоритм
Содержание
Предметный указатель
|

