




Вперед: 13.7.5 Отсеивание составных чисел
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.3 Всегда ли результатом работы Алгоритма являются простые числа?
Содержание
Предметный указатель
Основное время в процессе работы Алгоритма уходит на поиск
простых чисел в прогрессии 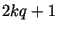 . Если Алгоритм наткнулся
на такое число, то проверка простоты его, в случае
справедливости условий теоремы 8, выполняется
сравнительно быстро. Поэтому важным качеством алгоритма
должна быть способность доказывать простоту каждого
простого числа, встречающегося в прогрессии. . Если Алгоритм наткнулся
на такое число, то проверка простоты его, в случае
справедливости условий теоремы 8, выполняется
сравнительно быстро. Поэтому важным качеством алгоритма
должна быть способность доказывать простоту каждого
простого числа, встречающегося в прогрессии.
Отметим, в этой связи, что не все простые числа  могут быть распознаны указанным алгоритмом. Другими
словами, перебирая последовательно четные числа
могут быть распознаны указанным алгоритмом. Другими
словами, перебирая последовательно четные числа  , и
проверяя числа , и
проверяя числа
 на простоту, Алгоритм
может не распознать некоторые простые числа на простоту, Алгоритм
может не распознать некоторые простые числа  и,
увеличив значение и,
увеличив значение 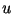 , продолжать работу дальше. Это,
конечно, может приводить к увеличению времени работы
алгоритма. Укажем некоторые примеры чисел , продолжать работу дальше. Это,
конечно, может приводить к увеличению времени работы
алгоритма. Укажем некоторые примеры чисел  , не
идентифицируемых Алгоритмом как простые. Простыми являются
все числа , не
идентифицируемых Алгоритмом как простые. Простыми являются
все числа  из следующего списка:
1) из следующего списка:
1)
 , ,  , ,
 ; ;
2)
 , ,  , ,
 ; ;
3)
 , ,  , ,
 ; ;
4)
 , ,  , ,
 ; ;
5)
 , ,
 , ,
 . .
Во всех указанных случаях 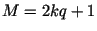 и имеют место сравнения и имеют место сравнения
 Значит, если одно из указанных чисел
Значит, если одно из указанных чисел  встретится в
Алгоритме как встретится в
Алгоритме как  , а соответствующие значения , а соответствующие значения  будут равны
будут равны  , то числа , то числа  не будут приняты как
простые не будут приняты как
простые  и Алгоритм продолжит работу. и Алгоритм продолжит работу.
Указанные примеры являются частными реализациями при
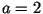 следующего общего утверждения. следующего общего утверждения.
Предложение 1.
Пусть 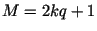 -- простое число, причем -- простое число, причем  простое и простое и
 . Если . Если
 , ,  , и порядок
числа , и порядок
числа  по модулю по модулю  не превосходит не превосходит  , то , то
 и, следовательно, простое число и, следовательно, простое число  не удовлетворяет условиям теоремы 8.
не удовлетворяет условиям теоремы 8.
Исключить указанный пропуск простых чисел можно за счет
проверки в Алгоритме условий теоремы 8 не только
при 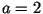 , но и при других значениях основания , но и при других значениях основания  . .
Предложение 2.
Для каждого простого числа 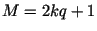 , ,
 , ,
 , на промежутке , на промежутке
 имеется не менее имеется не менее
 чисел чисел  , для которых
выполнены условия теоремы 8. , для которых
выполнены условия теоремы 8.
Предложение 2 показывает, что, выбирая
случайным образом числа  на промежутке на промежутке
 при простом при простом  , можно с вероятностью,
большей чем , можно с вероятностью,
большей чем
 , найти число , найти число  , для которого
будут выполнены условия теоремы 8. , для которого
будут выполнены условия теоремы 8.
Удобнее, однако, выбирать числа  последовательно: последовательно:
 . Увеличение продолжительности работы при этом
произойдет лишь для тех простых чисел . Увеличение продолжительности работы при этом
произойдет лишь для тех простых чисел  , которые
пропускались Алгоритмом. Но и для них, если принять на веру,
что корни сравнения , которые
пропускались Алгоритмом. Но и для них, если принять на веру,
что корни сравнения
 распределены
равномерно на промежутке распределены
равномерно на промежутке
 ,
необходимое для выполнимости теоремы 8 число ,
необходимое для выполнимости теоремы 8 число  будет найдено, согласно предложению 2,
достаточно быстро.
будет найдено, согласно предложению 2,
достаточно быстро.
Но как будет работать измененный алгоритм, если число
 составное? Существуют составные числа составное? Существуют составные числа  (числа
Кармайкла) для которых условие (2) выполняется
при любом (числа
Кармайкла) для которых условие (2) выполняется
при любом  , ,  , так же как и для простых чисел.
Эти числа встречаются достаточно редко. Тем не менее в
1993 г. доказано, что их бесконечно много. Известна
модификация теста теоремы 8,
основанная на следующей теореме: , так же как и для простых чисел.
Эти числа встречаются достаточно редко. Тем не менее в
1993 г. доказано, что их бесконечно много. Известна
модификация теста теоремы 8,
основанная на следующей теореме:
Теорема 10 ([Rab], [Will]).
Пусть M -- нечетное составное число,  , ,  нечетно, и
нечетно, и  -- множество натуральных чисел -- множество натуральных чисел  , ,
 , для которых выполнены условия:
1) , для которых выполнены условия:
1)
 , ,
2)
при всех  , ,

 Тогда количество элементов в
Тогда количество элементов в  не меньше не меньше  . .
Если  -- простое число, то для каждого -- простое число, то для каждого  , ,  ,
согласно малой теореме Ферма имеем ,
согласно малой теореме Ферма имеем
 т. е. для простого
т. е. для простого  хотя бы одно из условий
теоремы 10 обязательно нарушается. В то же время, как
следует из теоремы 9, для составного числа хотя бы одно из условий
теоремы 10 обязательно нарушается. В то же время, как
следует из теоремы 9, для составного числа  нарушение хотя бы одного из условий теоремы 9
происходит с вероятностью
нарушение хотя бы одного из условий теоремы 9
происходит с вероятностью
 при случайном выборе
при случайном выборе  на интервале на интервале  . При этом,
что легко видеть, выполняется сравнение (2).
Таким образом, если проверять для числа . При этом,
что легко видеть, выполняется сравнение (2).
Таким образом, если проверять для числа  выполнимость
условий 1) и 2) для выполнимость
условий 1) и 2) для  случайно выбранных значений случайно выбранных значений  ,
или, что технически удобнее, для ,
или, что технически удобнее, для
 , то с
вероятностью, большей, чем , то с
вероятностью, большей, чем 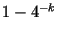 , составное число , составное число  будет при этом опознано как составное.
будет при этом опознано как составное.
Итак, изменим пункт 8 Алгоритма следующим образом:
8.1.
Положить
 . Вычислить целое . Вычислить целое  и нечетное число
и нечетное число  такие, что ( такие, что (
 . .
8.2.
Положить
 . .
8.3.
Проверить условие
 Если это условие нарушается, перейти в шаг 8.6.
Если это условие нарушается, перейти в шаг 8.6.
8.4.
При каждом  , ,
 ,
проверить условие ,
проверить условие
 Если оно нарушается хотя бы при одном
Если оно нарушается хотя бы при одном  , перейти в
шаг 8.6. , перейти в
шаг 8.6.
8.5.
Положить
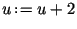 и перейти в пункт 6. и перейти в пункт 6.
8.6.
Проверить условие
 |
(8) |
Если это условие не выполняется, перейти в пункт 8.2.
8.7.
Проверить условие
 . Если это
условие не выполняется, перейти в пункт 8.2. . Если это
условие не выполняется, перейти в пункт 8.2.
8.8.
Положить
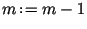 . .
Как уже было сказано, приведенное выше изменение пункта 8
Алгоритма позволит достаточно быстро доказывать как простоту
числа  , если оно простое, так и непростоту, если оно
составное. При простом , если оно простое, так и непростоту, если оно
составное. При простом  Алгоритм из пунктов 8.3 и 8.4
будет всегда переходить в пункт 8.6, и согласно
предложению 2 довольно быстро будет найдено
число Алгоритм из пунктов 8.3 и 8.4
будет всегда переходить в пункт 8.6, и согласно
предложению 2 довольно быстро будет найдено
число  , для которого выполнится условие (8).
Условие пункта 8.7 для простого числа , для которого выполнится условие (8).
Условие пункта 8.7 для простого числа  , конечно же,
будет выполнено. Так что Алгоритм попадет в пункт 8.8, а
затем перейдет к построению простого числа , конечно же,
будет выполнено. Так что Алгоритм попадет в пункт 8.8, а
затем перейдет к построению простого числа  . Если
же число . Если
же число  составное и нарушается хотя бы одно из
условий пунктов 8.3 и 8.4, то согласно следствию из
теоремы 9 для составное и нарушается хотя бы одно из
условий пунктов 8.3 и 8.4, то согласно следствию из
теоремы 9 для  не могут выполняться оба
условия пунктов 8.6 и 8.7. Но тогда Алгоритм перейдет в
пункт 8.2, будет вычислено новое значение не могут выполняться оба
условия пунктов 8.6 и 8.7. Но тогда Алгоритм перейдет в
пункт 8.2, будет вычислено новое значение  , с которым
будут проверяться условия пунктов 8.3 и 8.4. Согласно
теореме 10 довольно быстро будет обнаружено число , с которым
будут проверяться условия пунктов 8.3 и 8.4. Согласно
теореме 10 довольно быстро будет обнаружено число
 , для которого будут выполнены условия пунктов 8.3 и 8.4.
Тогда число , для которого будут выполнены условия пунктов 8.3 и 8.4.
Тогда число  будет определено как составное и из
пункта 8.6 Алгоритм перейдет к построению нового числа будет определено как составное и из
пункта 8.6 Алгоритм перейдет к построению нового числа
 . .





Вперед: 13.7.5 Отсеивание составных чисел
Вверх: 13.7 Анализ алгоритма построения больших простых чисел, изложенного в Стандарте (ГОСТ Р 34.10-94) "Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма"
Назад: 13.7.3 Всегда ли результатом работы Алгоритма являются простые числа?
Содержание
Предметный указатель
|

