




Вперед: 14. Односторонние функции и псевдослучайные генераторы
Вверх: 13. Методы построения больших простых чисел
Назад: 13.7.6 Замечания
Содержание
Предметный указатель
13.8 Алгоритм построения простых чисел
Описываемый ниже алгоритм построения больших простых чисел
является модификацией Алгоритма из раздела 13.7,
учитывающей высказанные в этом разделе замечания. Для его
работы требуется таблица всех нечетных простых чисел,
меньших  . Такая таблица легко может быть
составлена, например, проверкой делимости на нечетные
числа, не превосходящие 361 (ведь . Такая таблица легко может быть
составлена, например, проверкой делимости на нечетные
числа, не превосходящие 361 (ведь
 ). По
заданным целым числам ). По
заданным целым числам  , ,  и и  , ,  , ,  ,
предлагаемый алгоритм строит простые числа ,
предлагаемый алгоритм строит простые числа  и и  с
условиями с
условиями
 |
(11) |
Например, для  , ,  , ,
![$ Z=2^{[t/2]-1}$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1980.gif) , ,
![$ T=2^{[t/2]}$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1981.gif) получаются простые числа получаются простые числа  и и  , имеющие
битовую длину соответственно , имеющие
битовую длину соответственно 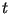 и и ![$ [t/2]$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1769.gif) . .
Алгоритм
1.
Вычислить две последовательности чисел
 где число
где число  выбрано так, что выбрано так, что
 . .
2.
Найти простое число  , удовлетворяющее
неравенствам , удовлетворяющее
неравенствам
 . Это можно сделать, перебирая
случайным образом нечетные числа на указанном промежутке
и проверяя их делимость на все простые, меньшие . Это можно сделать, перебирая
случайным образом нечетные числа на указанном промежутке
и проверяя их делимость на все простые, меньшие
 . .
3.

4.
Вычислить случайное число  на интервале на интервале
 и положить и положить
![$\displaystyle N=\left\lceil X_m/p_{m+1}\right\rceil+
\left[(X_m\cdot\xi)/p_{m+1}\right].
$](https://images.geo.web.ru/pubd/2001/10/10/0001161287/img1961.gif) (Здесь [x] и
(Здесь [x] и
 обозначают целую часть
числа обозначают целую часть
числа  и наименьшее целое, не меньшее, чем и наименьшее целое, не меньшее, чем  .) Если .) Если
 нечетно, положить нечетно, положить
 . .
5.
(В этом пункте алгоритма отсеиваются числа
 , делящиеся на 3 или на 5.)
5.1.
Положить , делящиеся на 3 или на 5.)
5.1.
Положить
 и для и для  , ,
 , ,  , ,  , ,  , ,  вычислить вычислить

5.2.
Если для всех  , ,
 , выполняется , выполняется  , перейти в пункт 6. , перейти в пункт 6.
5.3.
Положить
 и перейти в пункт 5.2.
и перейти в пункт 5.2.
6.
Вычислить
 . .
7.
Если
 , то перейти к пункту 4.
В противном случае проверить делимость числа , то перейти к пункту 4.
В противном случае проверить делимость числа  на все простые числа, не превосходящие
на все простые числа, не превосходящие  . В
случае делимости на какое-нибудь из указанных чисел перейти
в пункт 5.3. . В
случае делимости на какое-нибудь из указанных чисел перейти
в пункт 5.3.
8.
Ниже в этом пункте реализованы тесты проверки
на простоту, описанные в теоремах 9
и 10 из раздела 13.7).
8.1.
Положить
 . Вычислить целое . Вычислить целое
 и нечетное число и нечетное число  такие, что такие, что
 . .
8.2.
Положить
 . .
8.3.
Проверить условие
 Если это условие нарушается, перейти в пункт 8.6.
Если это условие нарушается, перейти в пункт 8.6.
8.4.
При каждом  , ,
 , проверить
условие , проверить
условие
 Если оно нарушается хотя бы при одном
Если оно нарушается хотя бы при одном  , перейти в пункт 8.6. , перейти в пункт 8.6.
8.5.
Перейти в пункт 5.3.
8.6.
Проверить условие
 Если это условие не выполняется, перейти в пункт 8.2.
Если это условие не выполняется, перейти в пункт 8.2.
8.7.
Проверить условие
 Если это условие не выполняется, перейти в пункт 8.2.
Если это условие не выполняется, перейти в пункт 8.2.
8.8.
Положить
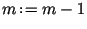 . .
9.
Если
 , то перейти к пункту 4. Если же , то перейти к пункту 4. Если же
 , то , то  и и  -- искомые простые числа. -- искомые простые числа.
Отметим, что простота числа  обеспечивается
теоремой 9 из
раздела 13.7. По этой же
теореме в силу неравенств обеспечивается
теоремой 9 из
раздела 13.7. По этой же
теореме в силу неравенств
 простым будет и число
простым будет и число  . .
Вышеописанный алгоритм был запрограммирован на языке
UBasic, в котором реализованы арифметические операции с
целыми числами величиной до  . Соответствующая
программа была применена для построения двух таблиц простых
чисел . Соответствующая
программа была применена для построения двух таблиц простых
чисел  и соответствующих простых делителей и соответствующих простых делителей  , ,
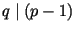 . В первой содержатся 20 простых чисел . В первой содержатся 20 простых чисел  ,
длина записи которых равна 512 битов, а во второй -- 15
чисел ,
длина записи которых равна 512 битов, а во второй -- 15
чисел  с длиной записи 1024 битов. На составление первой
таблицы персональный компьютер с процессором 80386/7
потратил 9 мин. 20 сек., а на составление второй --
30 мин. машинного времени. с длиной записи 1024 битов. На составление первой
таблицы персональный компьютер с процессором 80386/7
потратил 9 мин. 20 сек., а на составление второй --
30 мин. машинного времени.





Вперед: 14. Односторонние функции и псевдослучайные генераторы
Вверх: 13. Методы построения больших простых чисел
Назад: 13.7.6 Замечания
Содержание
Предметный указатель
|


 где число
где число  Если оно нарушается хотя бы при одном
Если оно нарушается хотя бы при одном  Если это условие не выполняется, перейти в пункт 8.2.
Если это условие не выполняется, перейти в пункт 8.2.
 простым будет и число
простым будет и число