4.2.2 Схема Шнорра [Sch]

Пусть участникам протокола известны некоторые простые числа , такие, что , , , а также случайный элемент порядка группы и криптографически стойкая односторонняя хэш-функция . Параметры , , и хэш-функция могут быть выбраны центром обеспечения безопасности. Подписывающий выбирает секретный ключ и вычисляет открытый ключ . Пространством сообщений в данной схеме является . Для генерации подписи для сообщения нужно выбрать и вычислить , и . Искомой подписью является пара . Параметр 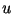должен быть секретным и может быть уничтожен после генерации подписи. Проверка подписи для сообщения сводится к проверке равенства .

Наиболее сложная операция, выполняемая при вычислении и проверке подписей в схемах типа Эль Гамаля -- это дискретное экспоненцирование . Преимущество схемы Шнорра перед схемой Эль Гамаля заключается в том, что 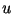выбирается из меньшего множества (длина 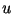 -- порядка 140 битов). Это повышает эффективность вычисления дискретных экспонент.

Кроме того, заметим, что использование в схеме Шнорра хэш-функции при вычислении и приведение подписи по модулю сокращают длину подписи по сравнению со схемой Эль Гамаля. Длина подписи -- один из важнейших показателей эффективности схемы.

Автор [Sch] предлагает также метод ускорения генерации подписей в вышеописанной схеме. Этот метод заключается в том, чтобы хранить (например, на интеллектуальной карточке) несколько пар , где , а (разные выбираются независимо друг от друга). При генерации подписи пара не вычисляется согласно вышеописанной схеме, а порождается как некоторая псевдослучайная комбинация пар . После этого набор обновляется псевдослучайным образом. Этот метод позволяет сократить количество вычислений дискретных экспонент. Однако конкретные алгоритмы его реализации должны быть секретными и различными для каждой интеллектуальной карточки.