|
Ю. И. Галушкин, Е. П. Дубинин,
А. А. Свешников, С. А. Ушаков
Московский государственный
университет им. М. В. Ломоносова, Музей
землеведения
Опубликовано:"Российский журнал
наук о Земле" том 2, N4, Декабрь 2000 |
Содержание |
Первая термическая модель, объяснявшая природу
генерального рельефа и теплового потока СОХ,
была предложена Д. МакКензи [McKenzie, 1967]. В ней распределение
температур, тепловой поток и рельеф поверхности
океанической литосферы определялись решением
стационарного уравнения теплопроводности для
литосферной плиты постоянной толщины,
движущейся с постоянной скоростью V от оси
хребта ( V - полускорость спрединга):
 |
(1) |
где K - коэффициент теплопроводности, r - плотность и СP -
теплоемкость пород литосферы; v - скорость
спрединга; T(x,z) - температура пород и
свободный член уравнения A(x,z) = 0.
Граничные условия имели вид: T=T0=0
при z=0 ; T=T1 на нижней границе
литосферы z=H ; T=T1 на оси x=0
и  T/ T/ x x 0 при x 0 при x 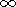 . Решение искалось в виде ряда Фурье и имело
вид [McKenzie, 1967]: . Решение искалось в виде ряда Фурье и имело
вид [McKenzie, 1967]:
 |
(2) |
Здесь T=(T1-T0)T +T0, x=Hx +T0, x=Hx , z=Hz , z=Hz и R=rCP vH/2k -
число Релея. В области x, где толщина
литосферы заметно отличается от
асимптотической, решение (2) близко к известному
решению для остывающего полупространства с
начальной температурой T=Ts=T1
[Карслоу, Егер, 1964]: и R=rCP vH/2k -
число Релея. В области x, где толщина
литосферы заметно отличается от
асимптотической, решение (2) близко к известному
решению для остывающего полупространства с
начальной температурой T=Ts=T1
[Карслоу, Егер, 1964]:
 |
(3) |
где F - функция вероятности и k=K/rCP -
термическая диффузия пород. Модель остывающего
полупространства (3) была использована в 1972 г.
О. Г. Сорохтиным, в нашей стране, и
Р. Паркером и Д. Олденбургом, за рубежом,
чтобы получить известные законы изменения
теплового потока:
 |
(4) |
и рельефа хребта, h, как 1/(t1/2) и
аналогичной зависимости для мощности
океанической литосферы: TL/TS = F(HL/(2(kx/v)1/2)),
которая определяется из (1) по соотношению T=TL
и предполагает рост толщины литосферы
пропорционально t1/2 (рис. 1)
[Сорохтин, 1973; Parker and Oldenburg,
1973]. Здесь TL -
температура, близкая к температуре солидуса
материала мантии литосферы и t=x/v -
возраст литосферы.
Модификацию решения Д. МакКензи для учета
эффекта выделения скрытой теплоты плавления
предпринял Д. Олденбург в моделях 1973 и 1975 гг.
Он искал распределение температур в
океанической литосфере в
рамках решения типичной задачи Стефана,
задавая на нижней переменной границе литосферы
температуру, равную температуре солидуса: z=HL(x)
при T=TL и определяя на этой границе
скачок теплового потока, обусловленный
выделением скрытой теплоты плавления материала
мантии: K(nx T/ T/ x
+ nz x
+ nz T/ T/ z) = -Lrv. Чтобы избежать особенности в
решении на оси хребта, вводилось дополнительное
условие при x =0 и 0 z) = -Lrv. Чтобы избежать особенности в
решении на оси хребта, вводилось дополнительное
условие при x =0 и 0 z z 1: -K( 1: -K( T/ T/ x)=rv[L+CP(TL-Tf)],
которое предполагало, что все тепло, приносимое
интрузиями в осевую зону, уносится
горизонтальным тепловым потоком. Выше l -
значения толщины литосферы на оси,
предполагаемое заранее, Tf - эффективная
температура интрузий, nx и nz -
компоненты вектора внешней нормали к нижней
границе литосферы HL(x). Задача
решается численно, но из характера решения
следует, что глубины изотерм, рельеф, тепловой
поток и мощность литосферы остаются функциями t1/2
и в этой модели решения. С удалением от оси, в
области x x)=rv[L+CP(TL-Tf)],
которое предполагало, что все тепло, приносимое
интрузиями в осевую зону, уносится
горизонтальным тепловым потоком. Выше l -
значения толщины литосферы на оси,
предполагаемое заранее, Tf - эффективная
температура интрузий, nx и nz -
компоненты вектора внешней нормали к нижней
границе литосферы HL(x). Задача
решается численно, но из характера решения
следует, что глубины изотерм, рельеф, тепловой
поток и мощность литосферы остаются функциями t1/2
и в этой модели решения. С удалением от оси, в
области x 2lK/rvCP, где 2lK/rvCP, где  2T/ 2T/  x2 x2  (rCP v/K)( (rCP v/K)( T)/( T)/( x), получается
асимптотическое решение, которое полностью
аналогично (3). x), получается
асимптотическое решение, которое полностью
аналогично (3).
Согласно асимптотическому решению, толщина
литосферы продолжала неограниченно расти как t
и для большого возраста океанической литосферы.
Однако, наблюдения показывают, что при возрасте
коры t>70 млн лет глубины изотерм и
поверхности дна океана, а также тепловой поток,
крайне медленно меняются с возрастом [Parson and
Sclater, 1977], качественно
согласуясь с моделью остывающей плиты McKenzie [1967]. Дж. Шуберт с соавторами [Schubert
et al., 1975] пытался исправить это
положение, рассматривая зависимость
коэффициента теплопроводности от температуры и
эффект выделения тепла вязкого трения в
основании литосферы, вызванного скольжением
последней в верхних слоях вязкой
астеносферы. Авторы установили, что если
теплопроводность пород мантии зависит только от
температуры, как, например, в работе [Schatz and Simmons,
1972], то глубины изотерм, тепловой
поток и рельеф поверхности литосферы будут
по-прежнему изменяться как функции t1/2.
Расчеты со значениями геофизических параметров,
типичных для пород мантии литосферы и
астеносферы, показали, что тепло вязкого трения
слабо сказывается на тепловом режиме литосферы
для полускоростей спрединга V5 см/год, в то
время как для V=10 см/год заметное отклонение
от закона t1/2 наблюдалось уже для возраста
литосферы t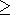 25 млн
лет, что также противоречит наблюдениям. Тогда,
чтобы снять противоречие, Д. Ольденбург [Oldenburg,
1975] предположил, что характер
конвективных движений в астеносфере и глубокой
мантии определяет некоторую постоянную величину
глубинного теплового потока из мантии с
удалением от оси спрединга, тем самым
устанавливая асимптотический тепловой режим
литосферы аналогично тому, как это имеет место и
в модели плиты постоянной толщины. 25 млн
лет, что также противоречит наблюдениям. Тогда,
чтобы снять противоречие, Д. Ольденбург [Oldenburg,
1975] предположил, что характер
конвективных движений в астеносфере и глубокой
мантии определяет некоторую постоянную величину
глубинного теплового потока из мантии с
удалением от оси спрединга, тем самым
устанавливая асимптотический тепловой режим
литосферы аналогично тому, как это имеет место и
в модели плиты постоянной толщины.
Хотя в целом рассмотренные модели неплохо
описывали генеральные черты изменения теплового
потока, рельефа дна и мощности океанической
литосферы с возрастом, однако продолжающиеся
геофизические исследования приносили новую
информацию о строении и геофизических полях
литосферы срединно-океанических хребтов, и
особенно их осевых зон. Открывшееся своеобразие
теплового потока, рельефа осевых долин и
поднятий, особенности гравитационных и
магнитных полей в осевых зонах хребта требовали
уточнения существующих тепловых моделей.
|

