|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
I.3.4. Частные случаи теоремы Эйлера
Для решения большинства
кристаллографических задач достаточно
ограничиться рассмотрением частного случая
теоремы Эйлера, т.е. взаимодействия осей 2-го
порядка - простых (L2) и (или)
инверсионных (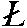 2 =
Р). В результате получим три варианта их
сочетаний - три теоремы взаимодействия осей: 2 =
Р). В результате получим три варианта их
сочетаний - три теоремы взаимодействия осей:
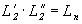 , ,
 ' 2 (Р' ' 2 (Р'  ) . ) . 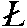 '' 2
(Р'' '' 2
(Р'' ) = Ln , ) = Ln ,
L2 . 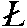 2 (Р 2 (Р ) = ) = 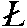 n (= n (= 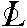 ' n ), ' n ),
для доказательства которых
инверсионную ось 2-го порядка удобно заменить на
перпендикулярную к ней зеркальную плоскость
симметрии (Р ). В данном случае нет
смысла обращаться к теоремам сферической
тригонометрии, а следует использовать модельное
доказательство, поскольку все построения
осуществляются на плоскости. ). В данном случае нет
смысла обращаться к теоремам сферической
тригонометрии, а следует использовать модельное
доказательство, поскольку все построения
осуществляются на плоскости.
Теорема 1. Взаимодействие двух
пересекающихся под углом 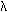 поворотных осей симметрии 2-го
порядка эквивалентно повороту вокруг
результирующей, также поворотной оси симметрии,
проходящей через точку их пересечения
перпендикулярно плоскости взаимодействующих
осей; при этом элементарный угол поворота a
результирующей оси вдвое превышает угол поворотных осей симметрии 2-го
порядка эквивалентно повороту вокруг
результирующей, также поворотной оси симметрии,
проходящей через точку их пересечения
перпендикулярно плоскости взаимодействующих
осей; при этом элементарный угол поворота a
результирующей оси вдвое превышает угол 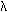 между
исходными осями: между
исходными осями:
  ( ( = 2 = 2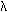 ). ).
.ля определения положения и
порядка порожденной оси воспользуемся модельным
доказательством (рис. 12, а). Так
как обе исходные оси - элементы симметрии 1-го
рода, то асимметричная фигура 1 дважды
преобразуется в конгруэнтную ей. Поэтому
результирующей операцией может быть лишь
операция симметрии 1-го рода - простой поворот:
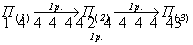 . .
Действительно, конгруэнтные фигуры 1 и
3 могут быть совмещены друг с другом поворотом
вокруг вертикальной оси Ln на угол  = 2 = 2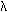 .
Возникшая ось перпендикулярна к плоскости
исходных осей 2-го порядка. При этом поворот будет
направлен в сторону от оси 1-го поворота ко 2-й оси,
т.е. в данном случае против часовой стрелки. .
Возникшая ось перпендикулярна к плоскости
исходных осей 2-го порядка. При этом поворот будет
направлен в сторону от оси 1-го поворота ко 2-й оси,
т.е. в данном случае против часовой стрелки.
Теорема 2. Взаимодействие двух
пересекающихся под углом 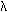 зеркальных плоскостей симметрии
эквивалентно простому повороту вокруг
результирующей оси симметрии, совпадающей с
линией их пересечения; при этом элементарный
угол поворота a этой оси вдвое превышает угол зеркальных плоскостей симметрии
эквивалентно простому повороту вокруг
результирующей оси симметрии, совпадающей с
линией их пересечения; при этом элементарный
угол поворота a этой оси вдвое превышает угол 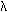 между
исходными осями: между
исходными осями:
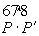 ( (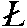 2 . 2 . 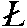 ' 2) = Ln
( ' 2) = Ln
( = 2 = 2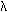 ). ).
.ак как порождающие плоскости -
элементы симметрии 2-го рода, то исходная фигура 1
при отражении в первой из них (Р)
преобразуется в энантиоморфную фигуру 2, а затем,
при последующем отражении в плоскости Р' ,
снова окажется в положении 3, конгруэнтном
начальному (рис. 12, б). Отсюда
результирующей операцией может быть лишь
операция 1-го рода - поворот:
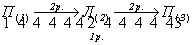 . .
Из рис. 12, б видно, что
"правая" фигура 1 и конечная 3, тоже "правая",
совмещаются друг с другом простым поворотом на
угол  = 2 = 2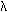 вокруг
оси Ln, являющейся линией пересечения
зеркальных плоскостей симметрии, в направлении
от плоскости 1-го отражения ко 2-й плоскости.
Поскольку нормали к зеркальным плоскостям
симметрии Р и Р' совпадают с
инверсионными осями вокруг
оси Ln, являющейся линией пересечения
зеркальных плоскостей симметрии, в направлении
от плоскости 1-го отражения ко 2-й плоскости.
Поскольку нормали к зеркальным плоскостям
симметрии Р и Р' совпадают с
инверсионными осями 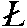 2
и 2
и 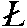 ' 2, их
взаимодействие даст тот же результат. ' 2, их
взаимодействие даст тот же результат.
Теорема 3. Взаимодействие
поворотной оси 2-го порядка и зеркальной
плоскости симметрии, пересекающихся под углом 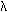 ,
эквивалентно действию зеркальной оси симметрии
с элементарным углом поворота ,
эквивалентно действию зеркальной оси симметрии
с элементарным углом поворота  = 2 = 2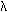 или соответствующей ей
инверсионной оси с элементарным углом поворота 180o
- или соответствующей ей
инверсионной оси с элементарным углом поворота 180o
-  : :
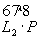 = = 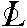 n (= n (=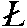 n' ) ( n' ) ( = 2 = 2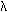 ). ).
если взаимодействуют операции
симметрии 1-го и 2-го рода, то результирующей
оказывается операция 2-го рода (рис. 12,
в). "Правая" фигура 1 осью L2
переводится в конгруэнтное положение 2, которое
после отражения в плоскости Р займет
положение 3, энантиоморфное исходному. "Правая"
(1) и "левая" (3) фигуры могут быть совмещены друг
с другом уже двумя симметрическими операциями -
поворотом на угол  = 2 = 2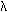 и отражением в зеркальной
плоскости, перпендикулярной оси поворота, -
составляющими операциями зеркальной оси
симметрии ( и отражением в зеркальной
плоскости, перпендикулярной оси поворота, -
составляющими операциями зеркальной оси
симметрии (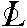 n ) либо
поворотом на угол 180o - n ) либо
поворотом на угол 180o -  в противоположную сторону и
"отражением" в точке (инверсией), совпадающей с
точкой пересечения исходных плоскости и оси. А
это уже составляющие операции инверсионной оси
симметрии в противоположную сторону и
"отражением" в точке (инверсией), совпадающей с
точкой пересечения исходных плоскости и оси. А
это уже составляющие операции инверсионной оси
симметрии 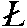 n ( где n ( где 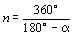 ): ):
 . .
.се три симметрические операции
в рассмотренных теоремах взаимосвязаны, т.е. для
каждой из теорем справедливы перестановки: за
порождающую можно принять любую пару
симметрических операций. Например, L2 .
P = 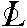 n , n , 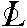 n . P = L2, n . P = L2, 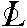 n . L2 = P и т.д. Однако обратные теоремы
невозможны, т.е. каждый порождающий элемент
симметрии может существовать самостоятельно,
без породивших его элементов симметрии. n . L2 = P и т.д. Однако обратные теоремы
невозможны, т.е. каждый порождающий элемент
симметрии может существовать самостоятельно,
без породивших его элементов симметрии.
В заключение необходимо отметить, что
все взаимодействия симметрических операций (а
следовательно, и сочетания элементов симметрии)
есть следствия и частные случаи приведенных выше
теорем, а точнее, одной фундаментальной осевой
теоремы Эйлера.
| 
