|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IV.5. Взаимодействие
плоскости симметрии и косо расположенной к ней
трансляции
Если трансляционный вектор 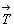 не перпендикулярен к
плоскости симметрии (рис. 27), то две
его компоненты - параллельная ( не перпендикулярен к
плоскости симметрии (рис. 27), то две
его компоненты - параллельная (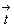 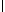 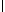 ) и ) и
перпендикулярная (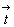  ) плоскости, на которые он может
быть разложен, взаимодействуют с плоскостью
по-разному. Трансляционная компонента,
параллельная плоскости ( ) плоскости, на которые он может
быть разложен, взаимодействуют с плоскостью
по-разному. Трансляционная компонента,
параллельная плоскости (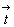 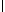 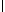 ), вольется в
нее и этим изменит характер ее скольжения (см. с.
47), а следовательно, и ее наименование,
перпендикулярная же составляющая ( ), вольется в
нее и этим изменит характер ее скольжения (см. с.
47), а следовательно, и ее наименование,
перпендикулярная же составляющая (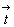  ) перенесет получившуюся
производную плоскость на свою середину (см. с. 50). ) перенесет получившуюся
производную плоскость на свою середину (см. с. 50).
Так, на рис. 27, а косо
расположенную по отношению к зеркальной
плоскости my трансляцию 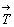 можно разложить на два составляющих
вектора: можно разложить на два составляющих
вектора: 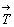 = = 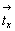 + + 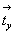 , где , где 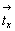 параллелен плоскости m
и параллелен плоскости m
и 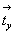 перпендикулярен к
ней. Первый, вливаясь в зеркальную плоскость,
превращает ее в плоскость скользящего отражения а,
второй переносит возникшую плоскость на свою
середину (рис. 28). То же справедливо
и для плоскостей иного наименования. Например,
при взаимодействии плоскости скользящего
отражения с (имеющей трансляционную
компоненту перпендикулярен к
ней. Первый, вливаясь в зеркальную плоскость,
превращает ее в плоскость скользящего отражения а,
второй переносит возникшую плоскость на свою
середину (рис. 28). То же справедливо
и для плоскостей иного наименования. Например,
при взаимодействии плоскости скользящего
отражения с (имеющей трансляционную
компоненту 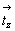 ) c косо
расположенным к ней вектором ) c косо
расположенным к ней вектором 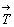 его составляющая, параллельная плоскости с
, превратит ее в клиноплоскость n, а
перпендикулярная перенесет возникшую плоскость n
на свою середину. В результате этого
взаимодействия плоскость с будет
чередоваться с клиноплоскостью n (рис.
27, б ). его составляющая, параллельная плоскости с
, превратит ее в клиноплоскость n, а
перпендикулярная перенесет возникшую плоскость n
на свою середину. В результате этого
взаимодействия плоскость с будет
чередоваться с клиноплоскостью n (рис.
27, б ).
|

