|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
VII.2.8. Графическое представление
некоторых пространственных групп
тетрагональной сингонии
Пространственная группа Р42 ( ) )
Наиболее просто вычерчиваются графики
пространственных групп тетрагональной
тетартоэдрии с единственной осью 4-го порядка.
Задав перпендикулярно фиксированной оси 42(z)
трансляционный координатный вектор (например,  ), оконтуриваем
элементарную ячейку, перенеся оси 42 в
ее вершины (рис. 87, а).
Взаимодействие оси 42 с заданным
вектором ), оконтуриваем
элементарную ячейку, перенеся оси 42 в
ее вершины (рис. 87, а).
Взаимодействие оси 42 с заданным
вектором  обусловит
появление оси того же наименования (42) в
центре одного из квадратов, построенных на этой
трансляции (см. с. 56). При этом в данном случае в
силу существования равноправных трансляционных
векторов вдоль всех четырех горизонтальных
координатных направлений (+ обусловит
появление оси того же наименования (42) в
центре одного из квадратов, построенных на этой
трансляции (см. с. 56). При этом в данном случае в
силу существования равноправных трансляционных
векторов вдоль всех четырех горизонтальных
координатных направлений (+  ,+ ,+  )
становится безразлично, в каком из построенных
на них квадратов (элементарных ячеек) появится
результирующая ось 42 (рис. 87,
б). )
становится безразлично, в каком из построенных
на них квадратов (элементарных ячеек) появится
результирующая ось 42 (рис. 87,
б).
Поскольку в группу 42 входит
операция поворота на 180o ( = 2), то взаимодействие оси 2z с
координатными горизонтальными трансляциями = 2), то взаимодействие оси 2z с
координатными горизонтальными трансляциями  и и  приведет к появлению результирующих осей 2
на их серединах (рис. 87, в) (см. с.
54). Таким образом, каждая из осей симметрии (2 и
42), входящих в состав пространственной
группы Р42 , взаимодействует с
трансляциями решетки по своему закону. Заметим,
однако, что результирующие оси оказываются
неэквивалентными исходным, т.е. не связанными с
ними трансляционными векторами решетки. приведет к появлению результирующих осей 2
на их серединах (рис. 87, в) (см. с.
54). Таким образом, каждая из осей симметрии (2 и
42), входящих в состав пространственной
группы Р42 , взаимодействует с
трансляциями решетки по своему закону. Заметим,
однако, что результирующие оси оказываются
неэквивалентными исходным, т.е. не связанными с
ними трансляционными векторами решетки.
Во всех пространственных группах,
подчиненных точечной группе 4, нет позиции
без степеней свободы, поэтому при выборе начала
координат (выборе точки с максимальной
симметрией) предпочтение отдается позициям на
осях 4-го порядка даже в том случае, когда эти оси
винтовые - 41, 42 или 43.
Пространственная группа 
Приняв за основу построенный график
пространственной группы Р42 (рис.
88, а), добавим к нему горизонтальную
плоскость n. В результате взаимодействия
исходной оси 42 с перпендикулярной к ней
клиноплоскостью n возникнет инверсионная ось
4-го порядка  в позиции в позиции  (см. с. 70 - 71) с особой
точкой на высоте (см. с. 70 - 71) с особой
точкой на высоте  (рис. 88, б). (рис. 88, б).
Поворотные оси 2-го порядка,
содержащиеся в осях 42 и  , взаимодействуя с перпендикулярной
к ним плоскостью n, дадут центры инверсии,
смещенные с точки пересечения оси и плоскости на
середины векторов , взаимодействуя с перпендикулярной
к ним плоскостью n, дадут центры инверсии,
смещенные с точки пересечения оси и плоскости на
середины векторов  , т.е.
в позицию , т.е.
в позицию  и т.д. (рис. 88, в). и т.д. (рис. 88, в).
В качестве начала координат в пр. гр.  предпочтен, однако, не
центр инверсии (с величиной симметрии 2), а более
высокосимметричная позиция также без степеней
свободы в особой точке инверсионной оси предпочтен, однако, не
центр инверсии (с величиной симметрии 2), а более
высокосимметричная позиция также без степеней
свободы в особой точке инверсионной оси  (величина симметрии 4) (рис. 88, г), при этом высоты
(координаты z) всех элементов симметрии
группы приводятся к выбранному началу координат. (величина симметрии 4) (рис. 88, г), при этом высоты
(координаты z) всех элементов симметрии
группы приводятся к выбранному началу координат.
Пространственные группы  и и 
Построение графика пространственной
группы  удобно начать с
вычерчивания графика ее подгруппы Р41.
Для этого, размножив исходную ось 41(z)
координатными трансляциями удобно начать с
вычерчивания графика ее подгруппы Р41.
Для этого, размножив исходную ось 41(z)
координатными трансляциями  и и  тетрагональной элементарной ячейки, получим еще
одну ось 41 в ее центре как результат
взаимодействия 41 .
тетрагональной элементарной ячейки, получим еще
одну ось 41 в ее центре как результат
взаимодействия 41 .  ( ( ) (рис. 89, а). Ось 21
= ) (рис. 89, а). Ось 21
=  , взаимодействуя с
координатными трансляциями, переместится на их
середины (рис. 89, б). , взаимодействуя с
координатными трансляциями, переместится на их
середины (рис. 89, б).
После введения горизонтальной
плоскости аz = mz . (где (где  ) ее
взаимодействие с винтовой осью 41 = 4 . ) ее
взаимодействие с винтовой осью 41 = 4 .
 (где (где  ), обусловит появление инверси-онной
оси ), обусловит появление инверси-онной
оси  . Для определения
положения оси . Для определения
положения оси  и высоты
ее особой точки необходимо учитывать не только
взаимодействие, но и действие операций
симметрии, состав-ляющих перечисленные
транс-ляционные элементы симмет-рии, друг на
друга [27]. Так, вектор и высоты
ее особой точки необходимо учитывать не только
взаимодействие, но и действие операций
симметрии, состав-ляющих перечисленные
транс-ляционные элементы симмет-рии, друг на
друга [27]. Так, вектор  -
трансля-ционная компонента винтовой оси 41
(рис. 90), будучи отраженным в
плоскости mz -
трансля-ционная компонента винтовой оси 41
(рис. 90), будучи отраженным в
плоскости mz  мнимой составляющей плос-кости скользящего
отражения az, перпендикулярной оси 41,
займет энантиоморфное положение (
мнимой составляющей плос-кости скользящего
отражения az, перпендикулярной оси 41,
займет энантиоморфное положение ( ) , и именно этот вектор (а не исходный
+ ) , и именно этот вектор (а не исходный
+ ) будет
взаимодействовать с инверсионной осью ) будет
взаимодействовать с инверсионной осью  , возникшей в результате
поворота на 90o и отражения в горизонтальной
плоскости. Особая точка указанной инверсионной
оси окажется на высоте , возникшей в результате
поворота на 90o и отражения в горизонтальной
плоскости. Особая точка указанной инверсионной
оси окажется на высоте  1. Дальнейшая судьба
инверсионной оси
1. Дальнейшая судьба
инверсионной оси  с
особой точкой на высоте с
особой точкой на высоте  будет определяться ее взаимодействием с
горизонтальной трансляционной компонентой
будет определяться ее взаимодействием с
горизонтальной трансляционной компонентой  плоскости аz:
окончательная ее позиция (см. рис. 89,
в) - в центре квадрата, построенного на
векторе плоскости аz:
окончательная ее позиция (см. рис. 89,
в) - в центре квадрата, построенного на
векторе  в сторону
вращения оси 41 (см. с. 56). С другой
стороны, на плоскость аz будет
действовать перпендикулярная к ней ось 41,
которая, развернув вектор в сторону
вращения оси 41 (см. с. 56). С другой
стороны, на плоскость аz будет
действовать перпендикулярная к ней ось 41,
которая, развернув вектор  на 90o и подняв его вдоль оси Z на на 90o и подняв его вдоль оси Z на  , превратит ее в плоскость
bz (см. рис. 89, г). Таким
образом, плоскость аz будет
чередоваться с плоскостью bz, что
обусловит появление дополнительного
трансляционного вектора в центр объема
элементарной ячейки - , превратит ее в плоскость
bz (см. рис. 89, г). Таким
образом, плоскость аz будет
чередоваться с плоскостью bz, что
обусловит появление дополнительного
трансляционного вектора в центр объема
элементарной ячейки -  .
В итоге задание лишь двух элементов симметрии - 41
и а .
В итоге задание лишь двух элементов симметрии - 41
и а -
приводит к объемноцентрированной решетке Браве
и в конечном счете к единственно возможной
пространственной группе -
приводит к объемноцентрированной решетке Браве
и в конечном счете к единственно возможной
пространственной группе 
В результате взаимодействия
центрирующего объем вектора  (где (где  ) и исходной
оси 41 = 4 . ) и исходной
оси 41 = 4 . (где (где  )
произойдет сложение их вертикальных
составляющих )
произойдет сложение их вертикальных
составляющих  . Это
изменит характер винтовой оси 41 на 43.
Последняя будет перенесена в центр квадрата,
построенного на горизонтальной составляющей . Это
изменит характер винтовой оси 41 на 43.
Последняя будет перенесена в центр квадрата,
построенного на горизонтальной составляющей  вектора вектора  в направлении вращения оси 41 (см.
с. 56), в результате чего ось 43 окажется в
позиции в направлении вращения оси 41 (см.
с. 56), в результате чего ось 43 окажется в
позиции  (см. рис. 89, г). При этом ось 21
вольется в качестве составляющей в полученную
ось 43. Взаимодействие инверсионной оси (см. рис. 89, г). При этом ось 21
вольется в качестве составляющей в полученную
ось 43. Взаимодействие инверсионной оси   с особой точкой на высоте
с особой точкой на высоте  с вектором с вектором  обусловит появление еще одной оси
обусловит появление еще одной оси  в позиции в позиции  с особой точкой на высоте
с особой точкой на высоте  (см.рис. 89, г). Центры
инверсии, возникшие как результат
взаимодействия осей 2-го порядка с
перпендикулярными плоскостями симметрии,
окажутся в позициях (см.рис. 89, г). Центры
инверсии, возникшие как результат
взаимодействия осей 2-го порядка с
перпендикулярными плоскостями симметрии,
окажутся в позициях   и и   (см. рис.
89, д). (см. рис.
89, д).
Начало координат выбираем в особой
точке инверсионной оси, например в точке с
координатами  , после
чего меняем на графике высоты всех центров
инверсии и особых точек, понижая их на , после
чего меняем на графике высоты всех центров
инверсии и особых точек, понижая их на  (см. рис. 89, е). (см. рис. 89, е).
Пространственная группа  
В качестве порождающих возьмем
пересекающиеся под углом 45o координатную
винтовую ось 21(x) и диагональную
плоскость скользящего отражения сd (рис. 91, а). Рассмотрим
взаимодействие и действие друг на друга
симметрических операций, составляющих заданные
элементы симметрии: 21(x) . сd
= 2x .  . md
. . md
. (где (где  , ,  ). ).
Взаимодействие 2x .md
приведет к появлению инверсионной оси  , особая точка которой
вектором , особая точка которой
вектором  сместится с
точки пересечения оси и плоскости на его
середину, т.е. на высоту сместится с
точки пересечения оси и плоскости на его
середину, т.е. на высоту  .
Однако положение оси будет зависеть не от
исходного вектора .
Однако положение оси будет зависеть не от
исходного вектора  , а
от его энантиоморфного аналога , а
от его энантиоморфного аналога , полученного отражением исходного
вектора + , полученного отражением исходного
вектора + в
плоскости md. В результате ось в
плоскости md. В результате ось  переместится в центр
квадрата, построенного на векторе переместится в центр
квадрата, построенного на векторе  в направлении, соответствующем
очередности проведенных симметрических
операций, т.е. от первого элемента симметрии 21(x)
ко второму, cd , и займет позицию ( в направлении, соответствующем
очередности проведенных симметрических
операций, т.е. от первого элемента симметрии 21(x)
ко второму, cd , и займет позицию ( ) (рис. 91, а).
Изменение очередности проводимых
симметрических операций на обратную ( ) (рис. 91, а).
Изменение очередности проводимых
симметрических операций на обратную ( ) приведет к
возникновению другой оси ) приведет к
возникновению другой оси  в центре квадрата, построенного на
исходном векторе в центре квадрата, построенного на
исходном векторе  .
Однако особая точка инверсионной оси .
Однако особая точка инверсионной оси  в этом случае будет
смещена на в этом случае будет
смещена на  уже не
вектором уже не
вектором  , а его
аналогом , а его
аналогом  , полученным
поворотом на 180o исходного вектора вокруг
поворотной составляющей оси 21(x) (рис. 91, а). Внеся координатными
трансляциями полученные оси , полученным
поворотом на 180o исходного вектора вокруг
поворотной составляющей оси 21(x) (рис. 91, а). Внеся координатными
трансляциями полученные оси  в исходную элементарную ячейку (рис. 91, б) и размножив ими заданные
плоскости с и ось 21(x), получим
весь комплекс горизонтальных осей 2-го порядка,
взаимодействие которых с координатными
векторами в исходную элементарную ячейку (рис. 91, б) и размножив ими заданные
плоскости с и ось 21(x), получим
весь комплекс горизонтальных осей 2-го порядка,
взаимодействие которых с координатными
векторами  , ,  и и  обусловит их периодичность через
половины указанных трансляций. обусловит их периодичность через
половины указанных трансляций.
Оси 2z =  , также взаимодействуя с векторами , также взаимодействуя с векторами  и и  , сместятся на их середины, т.е. в позиции , сместятся на их середины, т.е. в позиции 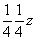 и и  (рис. 91, в), что наглядно
подтверждается результатом взаимодействия
взаимно перпендикулярных плоскостей с. (рис. 91, в), что наглядно
подтверждается результатом взаимодействия
взаимно перпендикулярных плоскостей с.
Выбор начала координат в
пространственной группе  в единственной позиции без степеней
свободы - особой точке инверсионной оси в единственной позиции без степеней
свободы - особой точке инверсионной оси  - не вызывает сомнений.
Соответствующее приведение высот (по оси Z) всех
элементов симметрии к выбранному началу
координат, а также нанесение клиноплоскостей n,
чередующихся с диагональными плоскостями с
(за счет взаимодействия с - не вызывает сомнений.
Соответствующее приведение высот (по оси Z) всех
элементов симметрии к выбранному началу
координат, а также нанесение клиноплоскостей n,
чередующихся с диагональными плоскостями с
(за счет взаимодействия с  = =  ),
приведет к окончательному графику данной
пространственной группы (рис. 91, г). ),
приведет к окончательному графику данной
пространственной группы (рис. 91, г).
Пространственные группы  и и 
Посчитав в качестве порождающих
координатную (my) и диагональную (d)
плоскости и нанеся их на график, рассмотрим
результат их взаимодействия. Для этого выпишем в
определенной последовательности все
симметрические операции, составляющие заданные
элементы симметрии:  (где
(где  , ,  , D - диагональ грани (001)
элементарной ячейки, , D - диагональ грани (001)
элементарной ячейки,  ).
Проведенные последовательно две операции
отражения в плоскостях mx и md,
расположенных под углом 45o друг к другу, дадут
ось 4-го порядка, характер которой задает
вертикальная составляющая плоскости d ( ).
Проведенные последовательно две операции
отражения в плоскостях mx и md,
расположенных под углом 45o друг к другу, дадут
ось 4-го порядка, характер которой задает
вертикальная составляющая плоскости d ( ), т.е. возникнет ось 41
с величиной скольжения ), т.е. возникнет ось 41
с величиной скольжения  . На положение результирующей оси 41
повлияет ее взаимодействие с перпендикулярной к
ней горизонтальной трансляционной составляющей
( . На положение результирующей оси 41
повлияет ее взаимодействие с перпендикулярной к
ней горизонтальной трансляционной составляющей
( ) клиноплоскости d:
она будет перенесена с линии пересечения
исходных плоскостей в центр квадрата,
построенного на ) клиноплоскости d:
она будет перенесена с линии пересечения
исходных плоскостей в центр квадрата,
построенного на  в
направлении очередности проводимых операций - от
плоскости my к плоскости d, и займет в
итоге положение в
направлении очередности проводимых операций - от
плоскости my к плоскости d, и займет в
итоге положение (рис. 92, а). (рис. 92, а).
Последовательность проведения
операций симметрии, обратная исходной ( ), скажется на ориентации
вектора ), скажется на ориентации
вектора  , который,
будучи отраженным в записанной вслед за ним
плоскости my, займет положение,
энантиоморфное исходному ( , который,
будучи отраженным в записанной вслед за ним
плоскости my, займет положение,
энантиоморфное исходному ( ). Этот отраженный вектор обусловит
винтовой характер и положение порожденной оси 43
в позиции ). Этот отраженный вектор обусловит
винтовой характер и положение порожденной оси 43
в позиции  (рис.
92, а), что подтверждается наличием
плоскости my, связывающей две
энантиоморфные оси 41 и 43 . (рис.
92, а), что подтверждается наличием
плоскости my, связывающей две
энантиоморфные оси 41 и 43 .
Результат не изменится и в том случае,
если вместо вектора + плоскости d использовать вектор -
плоскости d использовать вектор -  , направленный в
противоположную сторону (см. с. 63). Полученное
сочетание энантиоморфных осей 41 и 43
, так же как и присутствие диагональной
клиноплоскости d, подтверждает
объемно-центрированный тип решетки Браве. , направленный в
противоположную сторону (см. с. 63). Полученное
сочетание энантиоморфных осей 41 и 43
, так же как и присутствие диагональной
клиноплоскости d, подтверждает
объемно-центрированный тип решетки Браве.
Размножение осей 41 и 43
координатными трансляциями  и и  и их
взаимодействие с ними приведут к появлению в
центрах квадратов, построенных на этих
трансляциях, осей 4-го порядка такого же типа (рис. 92, б). и их
взаимодействие с ними приведут к появлению в
центрах квадратов, построенных на этих
трансляциях, осей 4-го порядка такого же типа (рис. 92, б).
Следующим шагом в построении графика
заданной пространственной группы может быть
размножение исходных плоскостей симметрии m
и d осями 41 и 43 (рис.
92, в), в результате чего получим
обязательную периодичность плоскостей одного
типа через половины трансляций,
перпендикулярных к ним. Взаимодействие
координатных плоскостей m с косо
расположенным к ним вектором  , обусловит чередование m(n). По
линии пересечения взаимно перпендикулярных
плоскостей mx и my возникнут
поворотные оси 2-го порядка, что хорошо
согласуется с расположением стрелок
клиноплоскостей d, направленных навстречу
друг другу в квадратах, центрированных
поворотными осями 2, и в одну сторону по
периметрам квадратов, центрированных осями 21
= , обусловит чередование m(n). По
линии пересечения взаимно перпендикулярных
плоскостей mx и my возникнут
поворотные оси 2-го порядка, что хорошо
согласуется с расположением стрелок
клиноплоскостей d, направленных навстречу
друг другу в квадратах, центрированных
поворотными осями 2, и в одну сторону по
периметрам квадратов, центрированных осями 21
=  (см. с. 129). (см. с. 129).
Таким образом, на промежуточной стадии
построения графика пр. гр.  оказался построенным график ее
гемиморфной подгруппы I41md (рис.
92, в), начало координат в которой выбирается
в моновариантной позиции mm2. оказался построенным график ее
гемиморфной подгруппы I41md (рис.
92, в), начало координат в которой выбирается
в моновариантной позиции mm2.
Завершаем построение вводом в
полученный график пр. гр. I41md
горизонтальной плоскости az,
взаимодействие которой с осями 41 и 43
, как было показано выше (см. с. 154), обусловит
появление в позициях, занятых полученными ранее
осями 2z ( и и  ), инверсионных осей ), инверсионных осей  с особыми точками на
высотах с особыми точками на
высотах  и и  соответственно, а также
центров инверсии (в позициях 000 и соответственно, а также
центров инверсии (в позициях 000 и  ) (рис. 92, г). ) (рис. 92, г).
Взаимодействие горизонтальных
плоскостей a(b) с вертикальными
плоскостями обеих позиций (m и d) даст
недостающий комплекс горизонтальных осей 2-го
порядка. Характер и положение диагональных осей
2-го порядка легко определить как результат
взаимодействий координатных плоскостей m с
инверсионными осями  ,
высоты особых точек которых укажут на высоты
диагональных поворотных осей 2-го порядка.
Возникновение диагональных винтовых осей 21
обязано как взаимодействию диагональных осей 2
с координатными трансляциями решетки, так и
присутствию вектора ,
высоты особых точек которых укажут на высоты
диагональных поворотных осей 2-го порядка.
Возникновение диагональных винтовых осей 21
обязано как взаимодействию диагональных осей 2
с координатными трансляциями решетки, так и
присутствию вектора  ,
взаимодействующему с полученными ранее
диагональными осями. ,
взаимодействующему с полученными ранее
диагональными осями.
Начало координат, естественно,
выбирается в самой высокосимметричной и
"неподвижной" точке (без степеней свободы): в
комплексе  , к
уровню которого затем и приводят высоты
остальных элементов симметрии вычерченной
пространственной группы , к
уровню которого затем и приводят высоты
остальных элементов симметрии вычерченной
пространственной группы  (рис. 92, д). (рис. 92, д).
Особо следует обратить внимание на
получение винтовых осей 41 и 43
на графиках родственных пространственных групп I41cd
и  , где обе
порождающие плоскости симметрии c и d
содержат вертикальные трансляционные
компоненты , где обе
порождающие плоскости симметрии c и d
содержат вертикальные трансляционные
компоненты  и и  соответственно.
Скользящие компоненты результирующих винтовых
осей 4-го порядка будут определяться знаком
(направлением) этих трансляционных компонент: соответственно.
Скользящие компоненты результирующих винтовых
осей 4-го порядка будут определяться знаком
(направлением) этих трансляционных компонент:  и и  . При этом в пространственных группах I41cd
и . При этом в пространственных группах I41cd
и  позиции осей 41
и 43 меняются местами по сравнению с их
расположением на графиках пр. гр. I41md и позиции осей 41
и 43 меняются местами по сравнению с их
расположением на графиках пр. гр. I41md и  (рис. 92, г,
д), т.е. направление "лопастей" винтовых осей
оказывается противоположным направлению
стрелок в обозначениях клиноплоскостей d,
указывающих на увеличение их вертикальной
трансляционной составляющей (см. с. 129). (рис. 92, г,
д), т.е. направление "лопастей" винтовых осей
оказывается противоположным направлению
стрелок в обозначениях клиноплоскостей d,
указывающих на увеличение их вертикальной
трансляционной составляющей (см. с. 129).
|

