Теория симметрии кристаллов

Рассмотренные выше двухмерные группы можно считать плоскими аналогами 230 федоровских (пространственных) групп симметрии. Список пространственных групп антисимметрии впервые предложен в 1953 г. А.М.Заморзаевым [35, 36], а в 1955 г. исправлен и дополнен Н.В.Беловым с соавторами [6, 11]. В итоге была выведена 1651 шубниковская группа симметрии, из них 230 полярных (классических), 230 нейтральных (серых) и 1191 черно-белая - собственно группы антисимметрии.

Вывод пространственных групп антисимметрии можно построить аналогично выводу одномерных и двухмерных групп, используя прием Н.В.Белова [6, 11]: взяв за основу 230 федоровских групп симметрии и добавив к каждой из них самостоятельную операцию антитождества 1', получим 230 нейтральных групп; остальные черно-белые группы (1191) получаются <зацвечиванием> как решеток Браве (517), так и подрешеточных элементов симметрии (674).

Рассмотрим возможности <зацвечивания> 14 решеток Браве, учитывая основное свойство цветной трансляции - 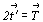(см. с. 266) и целесообразность введения дополнительных цветных узлов лишь в позиции, отвечающие симметрии вершинных узлов ячеек.

Ромбическая система

Рис. 160

Р-решетка. Цветная центрировка ребер ячейки какого-либо одного направления не имеет преимущества перед двумя другими и поэтому обозначена P'_s = P'_a = P'_b = P'_c (<s> - от англ. sceles - ребро) (рис. 160,1). Аналогично и центрировка одной пары противоположных граней может быть рассмотрена в любом аспекте: P'_C = P'_A = P'_B (рис. 160,2). Цветная центрировка объема приведет к оригинальной цветной ячейке - P'_I (рис. 160,3).

С-решетка. Цветная центрировка одного горизонтального ребра С-ячейки приведет к центрировке и другого ее ребра (вектор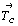!). Такая цветная решетка в различных аспектах будет иметь следующие символы: С'_a,b = A'_b,c = B'_a,c (рис. 160,4). Центрировка вертикальных ребер ячейки (с) приведет к центрировке и ее объема (рис. 160,5): C'_c,I = A'_a,I = B'_b,I. Цветная центрировка одной из вертикальных граней ячейки приведет за счет вектора 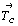к центрировке другой оставшейся пары граней (рис. 160,6): C'_A,B = A'_B,C= = B'_A,C .

Рис. 161

I-решетка. Центрировка ребер одного направления (b) приведет к центрировке грани (В), перпендикулярной этому ребру (рис. 160,7): I'_b,B = I'_a,A = I'_c,C .

F-решетка. Центрировка лишь одного ребра приведет к центрировке всех ребер и объема ячейки, т.е. к расположению цветных узлов во всех допустимых симметрией решетки позициях (рис. 160,8): F'_s = F'_a,b,c,I .

Итак, помимо 4-х типов классических решеток Браве ромбической сингонии для федоровских групп получили 8 центрированных цветных решеток для шубниковских групп - групп антисимметрии. Одновременная комбинированная центрировка ребер и объема, объема и граней и т.п. во всех типах ячеек приведет либо к уже выведенным цветным, либо к серым решеткам.

Р-решетка. <Зацвечивание> исходной Р-решетки (в рациональной установке 90^o ) приведет к трем примитивным цветным решеткам (рис. 161): P'_c , P'_b= P'_a , P'_B= P'_A. (В классической - минералогической - установке ( 90^o ) обозначение указанных решеток соответственно: P'_b , P'_c = P'_a , P'_C = P'_A).

B-решетка. <Зацвечивание> В-решетки даст две бокоцентрированные: центрировка горизонтального ребра (b) приведет и к центрировке ее объема, т.е. к B'_b,I = A'_a,I (рис. 161). Центрировка вертикального ребра (с) обусловит центрировку и ребра а ячейки, т.е. получим B'_a,c = A'_b,c (рис. 161). В итоге в моноклинной системе к двум классическим решеткам Браве добавилось 5 цветных.

Рис. 162

В решетках триклинной системы из-за произвольного выбора ребер ячейки все типы центрировок (P'_C , P'_I и т.д.) могут быть сведены к одному - P'_s (рис. 162).

Р-решетка. Цветная центрировка тетрагональной Р-решетки приводит к трем цветным: P'_c , P'_C и P'_I .

I-решетка. Центрировка в I-ячейке ее вертикальных ребер (с) приведет к одновременной цветной центрировке и ее базиса (С), т.е. к I'_c,C (рис. 163, а).

Гексагональная система

Рис. 163

Р-решетка. В гексагональной Р-решетке целесообразно вводить цветные узлы лишь в позиции на серединах вертикальных ребер ячейки (с) - единственные позиции с симметрией 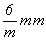. В результате получим P'_c (рис. 163, б).

R-решетка. В дважды объемноцентрированной R-решетке для введения цветных узлов пригодны лишь позиции на осях 3-го порядка с симметрией 3m - R'_c. В ромбоэдрическом - миллеровском - аспекте цветной вектор окажется центрирующим объем основной ячейки - объем примитивного ромбоэдра. В этом случае цветная решетка (но не ячейка Браве!) получит обозначение R'_I (= R'_c).

Цветная центрировка трех исходных классических кубических ячеек Браве - Р, I и F - приведет лишь к двум цветным: P'_I и F'_s (рис. 163, в). Действительно, центрировка ребер Р-ячейки приведет к F'_a,b,c,I ; центрировка граней Р-ячейки, так же как ребер или граней I-ячейки, приведет к серой Р-ячейке меньшего размера.

Таким образом, помимо 14 классических решеток Браве существуют 22 цветные пространственные решетки:

триклинной сингонии - Р, P'_s ,

моноклинной сингонии - P, P'_c , P'_b = P'_a , P'_B = P'_A ,

ромбической сингонии - Р, P'_s = P'_a = P'_b = P'_c , P'_A = P'_B = P'_C, P'_I,

C, C'_a,b, = A'_b,c= B'_a,c , C'_c,I = A'_a,I = B'_b,I ,

C'_A,B = A'_B,C= B'_A,C ,

F, F'_s = F'_a,b,c,I ,

тетрагональной сингонии - Р, P'_c, P'_C, P'_I ,

I, I'_c,C ,

гексагональной сингонии - Р, P'_с ,

R, R'_c ,

кубической сингонии - P, P_I',