|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
IX.5. Вывод двухмерных групп
антисимметрии
К 17 классическим двухмерным группам
симметрии 1 - 17 полярным
плоским группам для одноцветных слоев,
обладающим одним из каких-либо двух
противоположных качеств (или свойств) (рис. 149), добавим в качестве
самостоятельной операции антитождество 1',
что приведет к 17 нейтральным (серым) группам.
Например, pmm2 --> pmm2 . 1', p4bm --> p4bm . 1'
и т.д. (табл. 6)
Двухмерные группы антисимметрии
смешанной полярности, так же как и одномерные,
можно разделить на два семейства: с простой
(классической) решеткой, но с черно-белыми
подрешеточными элементами симметрии и с цветной
решеткой. По-разному "зацветив" порождающие
элементы симметрии в 15 исходных полярных группах
(за исключением групп р1 и р3), получим
первое семейство: 26 двухмерных черно-белых
(шубниковских) групп (табл. 6, рис. 150). Например, pmm2 --> pm' m2' (= pmm' 2') и
pm' m' 2, p4bm --> p4' b' m, p4' bm' и p4b' m'.
Прежде чем перейти к выводу групп
второго семейства - групп с антипереносами,
необходимо вывести двухмерные цветные решетки.
Для этого, взяв за основу 5 разных по симметрии
плоских решеток (см. рис. 53), следует
выяснить возможные позиции в них для цветных
узлов и этим определить типы цветных
центрировок. Поскольку дважды повторенный
антиперенос 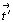 приводит к классической трансляции
приводит к классической трансляции 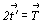 , то цветные узлы можно
ожидать на середине последней, т.е. на серединах
ребер плоской ячейки (параллелограмма) и в ее
центре. Так как дополнительный узел должен быть
трансляционно идентичным вершинному, т.е. может
располагаться только в позициях с симметрией
вершинного узла, то за отсутствием таковых в
плоской решетке с симметрией р6mm она цветной
быть не может. , то цветные узлы можно
ожидать на середине последней, т.е. на серединах
ребер плоской ячейки (параллелограмма) и в ее
центре. Так как дополнительный узел должен быть
трансляционно идентичным вершинному, т.е. может
располагаться только в позициях с симметрией
вершинного узла, то за отсутствием таковых в
плоской решетке с симметрией р6mm она цветной
быть не может.
В решетке с симметрией р112 нет
принципиальной разницы в центрировке разных
ребер ячейки (см. цветную вставку, рис.
151,1), как нет смысла и в центрировке самой
ячейки (ее базиса), ибо возможность произвольного
выбора координатных направлений (из-за
отсутствия горизонтальных особых направлений)
не сделает ее оригинальной (рис. 151,2).
Таким образом, p'a = p'b = p'С 2 . Одновременная центрировка двух
ребер ячейки (рис. 151,3) или одного
ребра и ее базиса (рис. 151,4) приведет
к возникновению классической трансляции 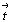 , т.е. к возможности
выбора ячейки p'b (или p'a ) вдвое
меньшего размера. Одновременная , т.е. к возможности
выбора ячейки p'b (или p'a ) вдвое
меньшего размера. Одновременная
центрировка и ребер и базиса ячейки (рис. 151,5) приведет к вдвое меньшим
"серым" трансляциям, т.е. к нейтральной (серой)
группе.
В ячейке с симметрией pmm2
ограниченный набор особых направлений, не
позволяющий выбрать ячейку по-иному, приводит к
двум типам центрировок (см. цветную вставку, рис. 152, 1, 2): p'a = p'b и p'C
. Одновременная цветная центрировка обоих
ребер ячейки (рис. 152,3) приведет к
возникновению классической трансляции,
центрирующей базис ячейки, т.е. к другому типу
решетки - с'а,b . Центрировка же центра
ячейки
и ее ребер (рис. 152,4), как и
в предыдущем случае, приведет к "серым"
трансляциям и, соответственно к выбору ячейки
меньшего размера.
Центрировка одного ребра (а) ячейки
с симметрией cmm2 (рис. 153,а)
приводит к автоматической центрировке другого
ее ребра (b). В результате получим лишь один
вариант цветной решетки - с'a,b = c'.
Центрировка диагонального вектора 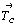 бессмысленна, ибо на
нем отсутствуют позиции, равные по симметрии
вершинному узлу. бессмысленна, ибо на
нем отсутствуют позиции, равные по симметрии
вершинному узлу.
В решетке с симметрией р4mm
центрировка одного ребра (a) ячейки (рис. 153, б) приведет к центрировке
и другого ее ребра (b) (ось 4!), т.е. к
появлению новой, более короткой классической
трансляции, центрирующей ячейку, а
следовательно, и к возможности выбора
примитивной ячейки меньшего размера - р'С .
В итоге к 5 классическим двухмерным
решеткам добавилось 5 типов черно-белых (цветных)
решеток:
моноклинной сингонии - p, p'a = p'b
= p'C ,
ромбической сингонии - p, p'a = p'b,
p'C ,
c, c'a,b = c',
тетрагональной сингонии - p, p'C ,
гексагональной сингонии - p.
В результате количество плоских групп
антисимметрии с антипереносами увеличилось до 20
(см. табл. 6 и рис. 150). Следует иметь в виду, что
введенный антиперенос, взаимодействуя со всеми
классическими элементами симметрии группы,
обусловит чередование (или тождественное
равенство) классических элементов и элементов
антисимметрии. Например, p'ab(b') a  m' 2(2'). Примеры
проекций двухмерных групп, изоморфных группам pba2
и cmm2, приведены на рис. 154 и 155 (см. цветную вставку). m' 2(2'). Примеры
проекций двухмерных групп, изоморфных группам pba2
и cmm2, приведены на рис. 154 и 155 (см. цветную вставку).
80 шубниковских двухмерных групп,
включающих 17 полярных (классических), 17
нейтральных (серых) и 46 собственно групп
антисимметрии, проиллюстрированы черно-белыми
мозаиками в "Атласе кристаллографических групп
симметрии" А.В.Шубникова [52](рис. 156).
Группы симметрии изображены в нем конгруэнтными
или энантиоморфными асимметричными фигурками
(белыми и черными - заштрихванными -
треугольниками ) (рис. 157, а, б).
При наложении друг на друга белого и
черного треугольников возникает нейтральная
фигура "серого" цвета, обозначенная в
"Атла-се " черной точкой (рис. 157, в).
Крапом показано свободное, не занятое фигурами
пространство. Каждая группа симметрии
представлена одной элементарной ячейкой.
В качестве примера опишем симметрию
некоторых мозаик. На рис. 158, а
(см. цветную вставку) (см. также рис. 156,
16) легко обнаруживаются центрирующая базис
ячейки трансляция 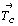 ,
две взаимно перпендикулярные плоскости
симметрии - m'x и my, одна из
которых цветная, и как результат их
взаимодействия - цветные оси 2-го порядка 2'z.
Взаимодействие m'x . ,
две взаимно перпендикулярные плоскости
симметрии - m'x и my, одна из
которых цветная, и как результат их
взаимодействия - цветные оси 2-го порядка 2'z.
Взаимодействие m'x . 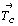 приведет к чередованию
m'x(b'x), my . приведет к чередованию
m'x(b'x), my . 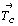 --> my(ay), 2'z . --> my(ay), 2'z .
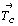 --> 2'z(2'z).
В результате имеем шубниковскую группу (группу
смешанной полярности с простой с-решеткой): сm'
m2' = cm' (b') m(a) 2' (2') (рис.
158, б). Следует обратить внимание на то, что
количество треугольников обоих сортов
(заштрихованных и пустых) в элементарной ячейке
соответствует порядку данной группы
антисимметрии. --> 2'z(2'z).
В результате имеем шубниковскую группу (группу
смешанной полярности с простой с-решеткой): сm'
m2' = cm' (b') m(a) 2' (2') (рис.
158, б). Следует обратить внимание на то, что
количество треугольников обоих сортов
(заштрихованных и пустых) в элементарной ячейке
соответствует порядку данной группы
антисимметрии.
Рис. 159, а (см. цветную
вставку) (см. также рис. 156, 41) иллюстрирует ромбическую группу с
цветной решеткой p'b и классическим
набором элементов симметрии: bx , my
и 2z. При этом за счет взаимодействия с
цветной трансляцией 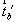 возникает тождественность bx
возникает тождественность bx 
m'x и чередование my(m'y)
и 2z(2'z), т.е. получим группу
антисимметрии p'b bm2 = p'b b  m' m(m') 2(2'). Обратим
внимание на то, что "зацвечивание" удваивает
порядок группы симметрии (например, порядок
группы pbm2, равный четырем, повышается до
восьми в группе p'bbm2). m' m(m') 2(2'). Обратим
внимание на то, что "зацвечивание" удваивает
порядок группы симметрии (например, порядок
группы pbm2, равный четырем, повышается до
восьми в группе p'bbm2).
Треугольники, снабженные черными
точками на рис. 159, б (см. также рис. 156, 24), указывают на
нейтральную (серую) группу антисимметрии - pb11.
1'. Присутствие самостоятельной операции
антитождества 1' также удваивает порядок
группы (например, порядок группы pb11 равен 2, pb11.
1' - 4).
Тетрагональная примитивная ячейка
изображена на рис. 159, в (см.
также рис. 156, 60).
Результатом взаимодействия координатных
плоскостей симметрии с диагональными (m'(g'))
будет ось антисимметрии 4-го порядка (4' ).
Шубниковская группа - p4' bm'. Порядок
классической подгруппы подтверждается
количеством треугольников - одноцветных (4) и
разноцветных (8).
|

