Теория симметрии кристаллов

Рис. 146

Свойствами антисимметрии могут обладать не только конечные фигуры, но и бесконечные постройки - одномерные [8], двухмерные [34] и трехмерные.

Взяв за основу 7 классических (полярных) одномерных групп симметрии: р111, р112, pm11, p1m1, pmm2, p1a1, pma2 (см. с. 71) - и добавив к ним антитождество 1' как самостоятельную операцию симметрии, получим нейтральные (серые) группы: р111 ^. 1', р112 ^.1', pm11 ^. 1', p1m1 ^. 1', pmm2 ^. 1', p1a1 ^. 1', pma2 ^. 1'. Заметим, что трансляция как элемент симметрии будет одновременно и классической и "цветной", т.е. в результате серой.

Для получения одномерных групп антисимметрии смешанной полярности необходимо учесть возможность "зацвечивания" как подрешеточных элементов симметрии (плоскостей и осей симметрии), так и самой решетки. В результате получим два семейства одномерных групп антисимметрии: 1 - с простой классической решеткой, но с <зацвеченными> подрешеточными элементами симметрии, 2 - с цветной решеткой.

Рис. 147

Возможность в первом семействе по-разному <зацвечивать> порождающие элементы симметрии в исходных полярных группах рmm2 1 и pma2 приведет к десяти черно-белым группам (рис. 146): pm'11, p1m'1, p112', p1a'1, pm' m2', pmm' 2', pm' m' 2, pm' a2', pma' 2', pm'a' 2, не содержащим операций антитождества 1' и антипереносов.

Второе семейство черно-белых одномерных групп симметрии отличается от первого наличием цветной трансляции - антипереноса. Поскольку дважды повторенная операция антисимметрии, в данном случае антитрансляция 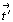, приводит к классической трансляции удвоенной длины (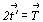) (см. цветную вставку, рис. 147), то получение различных по симметрии черно-белых бордюров сводится к вводу цветной трансляции 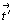, т.е. к <зацвечиванию> классических одноцветных орнаментов. Действительно, добавляя цветную трансляцию к семи полярным группам (<зацвечивая> решетку р' ), получим такое же количество одномерных черно-белых групп - групп с антипереносами (см. цветную вставку, рис. 148): p' 111, p' m11, p' 1m1, p' 112, p' mm2, p' 1a1, p' ma2.

Рис. 148

При этом следует помнить, что черно-белая трансляция будет взаимодействовать с элементами симметрии исходной группы. В результате возникнет чередование классических и цветных элементов симметрии, что делает бессмысленным одновременное <зацвечивание> как решетки, так и подрешеточных элементов симметрии.

Например, взаимодействие черно-белой трансляции 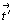и перпендикулярной к ней плоскости или оси симметрии приведет в группах p' mm2 и p' ma2 к чередованию - m(m') и 2(2') (см. рис. 148). Добавление же 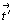к совпадающим с ней плоскостям 2-й позиции символа - m или а - превратит их в а' и m' соответственно, т.е. m a', a m' (где < > - знак тождественного равенства). Таким образом, развернутая запись указанных групп следующая:

p' mm2 = p' m(m') m a' 2(2'), p' ma2 = p' m(m') a m' 2(2').

В результате придем к 31 одномерной группе антисимметрии - шубниковской группе из семи полярных (классических) групп, семи нейтральных (серых) групп, семи групп смешанной полярности с "цветной" решеткой и десяти групп смешанной полярности с классической решеткой.

С помощью этих групп можно описать односторонние, бесконечные в одном направлении узоры (постройки) - бордюры. Все перечисленные группы не содержат "переворачивающих" симметрических операций, т.е. все элементы бордюра обращены к наблюдателю одной (лицевой) стороной. Если ввести в группы бордюров "переворачивающие" элементы симметрии - горизонтальные плоскости, оси симметрии или центр инверсии, то получим 31 группу симметрии двухсторонних лент. При этом черный и белый цвет фигур символизирует их лицевую и изнаночную стороны. Серые фигуры принято обозначать (отмечать) точкой (например ; pa'11 = p2₁ 11, см. рис. 156).