Теория симметрии кристаллов

XI.1. Симметрия плотнейших упаковок

Рис. 178

Кристаллические структуры многих веществ построены по принципу плотнейших шаровых упаковок, так как минимум потенциальной энергии кристаллической структуры отвечает геометрическому условию как можно более плотной укладки образующих ее частиц (структурных единиц - атомов, ионов и т.п.). Тенденция к образованию плотнейших и плотных упаковок свойственна всем типам кристаллических структур, но наиболее выражена в соединениях с металлической и ионной связью.

Симметрия плотнейшей упаковки влияет на симметрию всей кристаллической постройки. При этом, если кристаллические структуры простых веществ просто наследуют симметрию той или иной плотнейшей упаковки, то в более сложных соединениях наиболее объемные компоненты образуют одну из плотнейших упаковок и, как писал Н.В.Белов [4], "все разнообразие минерального кристаллического мира сводится к различным способам заселения пустот в ней", что естественно отражается и на симметрии всей постройки. Таким образом, теория плотнейших упаковок шаров одинакового размера оказалась очень продуктивной и удобной при описании построенных по ее законам кристаллических структур и определении их симметрии. Симметрия плотнейших упаковок подробнейшим образом разобрана в книге Н.В.Белова "Структура ионных кристаллов и металлических фаз" [4].

В объемном плотноупакованном слое, где каждый шар окружен шестью себе подобными (рис. 178), можно выделить две различные по симметрии позиции: 1) в центре каждого шара А (атома), описываемую точечной группой , и 2) в центрах треугольников В и С - центрах лунок, образованных тройками шаров - .

Симметрия пространственных плотнейших упаковок зависит от характера расположения плотноупакованных слоев относительно друг друга. При этом плотнейшая упаковка будет реализовываться лишь в том случае, если шары следующего слоя расположатся в лунках предыдущего. Однако из шести лунок, окружающих каждый шар исходного слоя, занятыми могут быть лишь половина, поскольку число лунок в плотнейшем слое, как видно из рис. 178, вдвое превышает число шаров в этом слое. И поскольку шары верхнего слоя могут попасть либо в лунки В, либо в лунки С, один слой относительно другого может быть ориентирован двояко. Следовательно, оригинальными окажутся лишь три положения плотноупакованных слоев: А, В и С. В результате любое сочетание этих трех букв (слоев) при условии, что две одинаковые не будут стоять рядом, дадут все разнообразие плотнейших упа-ковок с одинаковой степенью заполнения пространства шара-ми одного размера - 74,05%.

Очевидно, что при любом вышеописанном сочета-нии слоев будет сохраняться минимальная симметрия Р3m1. Действительно, при наложении шара (с симметрией ) в лунку предыдущего слоя (с симметрией ) сохранится лишь общая подгруппа с вертикальными элементами симметрии - Р3m1. Именно такой симметрией будет обладать произвольная укладка слоев, ибо горизонтальная плоскость симметрии групп и сохранится лишь при зеркальном расположении выше и ниже лежащих относительно исходного слоев. Соответственно и порядок групп симметрии различных упаковок будет кратен порядку группы Р3m1.

Если ограничиться определенным периодом повторяемости слоев А, B, С, то возникнут n-слойные упаковки, симметрия которых может быть более высокой, чем Р3m1. Однако во всех случаях она будет кратна порядку этой пространственной группы. Таким образом, легко перечислить 8 пространственных групп симметрии, с помощью которых можно описать все разнообразие плотнейших упаковок: Р3m, , R3m, , P6₃ mc, , , , среди которых лишь одна подчинена классу и описывает симметрию трехслойной - единственной кубической - плотнейшей упаковки. В то же время остальные пространственные группы гексагональной сингонии описывают большое количество упаковок с различными периодами.

Для определения симметрии плотнейших упаковок с заданным числом слоев (n) удобно прибегнуть к символике, предложенной Н.В.Беловым [2, 4 ]¹ , где каждая из букв "А", "В", "С" заменена буквами "г" или "к". При этом буква "г" обозначает слой, расположенный между двумя одинаковыми слоями (буквами), как любой слой в гексагональной упаковке; буква "к" обозначает слой между разными соседними слоями, как любой слой в кубической упаковке. В результате двухслойная гексагональная плотнейшая упаковка ...[АВ]ABAB... запишется как ...[гг]гг..., трехслойная кубическая упаковка ...[ABC]ABC... - как ...[ккк]ккк..., четырехслойная (топазовая) ...[ABAC]ABAC... - как ...[кгкг]кгкг..., шестислойная (рамзаитовая) ...[ABCACB]ABCACB... - как ...[гккгкк]гккгкк... и т.д.

С одной стороны, такой способ обозначения позволяет установить тождественность плотнейших упаковок, имеющих разные обозначения буквами "А", "В", "С". Например, кажущиеся на первый взгляд разными упаковки ...[ABABABC]... и ...[BCBCABC]... представляют одну и ту же упаковку ...[гггкккг]... и т.д. С другой стороны, анализ последовательности слоев (букв) "к" и "г" позволяет легко установить симметрию любой упаковки. Для этого определяются характерные для каждого сочетания букв (слоев) элементы симметрии, которые, будучи добавленными к всегда присутствующему в плотнейших упаковках комплексу Р3m1, укажут на пространственную группу данной упаковки.

Так, если слой "г" разбивает буквенную последовательность (формулу плотнейшей упаковки) на две зеркально равные части, то через шары этого слоя проходит горизонтальная зеркальная плоскость симметрии m_z, перпендикулярная главной оси. Центры инверсии лежат либо в слоях "к", либо между одинаковыми слоями ("кк" или "гг"), если соответствующая буква "к" или пара одинаковых букв рассекает формулу упаковки на две зеркально равные части.

Отсюда, обозначив зеркальные плоскости симметрии двойными линиями (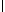 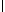), а центры инверсии звездочками (* ) и нанеся их рядом с буквенной последовательностью определенной плотнейшей упаковки, получим для двухслойной упаковки

Легко увидеть, что добавление к обязательному комплексу элементов симметрии любой упаковки Р3m1 горизонтальной плоскости m_z , проходящей через шары каждого плотноупакованного слоя и расположенного между слоями центра инверсии, приведет к гексагональной голоэдрической группе : Р3m1 + m_z + --> . Расположение центров инверсии между плоскостями симметрии m_z указывает на присутствие перпендикулярной им винтовой оси 2_1(z), уводящей с плоскости симметрии. О примитивности элементарной ячейки свидетельствуют два уровня расположения шаров плотнейшей упаковки вдоль оси с ячейки.

Для трехслойной упаковки

добавление центров инверсии, расположенных как между слоями "к", так и в самом слое "к", привело бы к центросимметричной пространственной группе . Однако наличие трех уровней расположения шаров плотнейшей упаковки относительно параметра с элементарной ячейки указывает на присутствие трансляции ромбоэдрической ячейки, т.е. на пр. гр. . Выделив в трехслойной плотнейшей упаковке ячейку, построенную на трех минимальных трансляционных векторах, убеждаемся в том, что это ромбоэдр с углом 60^o - основная ячейка гранецентрированного куба. К этому же выводу приходим и определив симметрию координационного полиэдра вокруг любого шара рассматриваемой трехслойной упаковки, представленного 12-вершинником - архимедовым кубооктаэдром, фигурой не с одной, а с четырьмя осями 3-го порядка и тремя осями 4-го, т.е. многогранником, указывающим на более высокую - кубическую - симметрию данной упаковки. В результате приходим к новой координатной системе, обслуживающей указанное расположение шаров, т.е. к симметрии не ромбоэдрической (), а кубической () с гранецентрированной решеткой Браве, где шары расположены по кубическому гранецентрированному закону.

В четырехслойной - топазовой - плотнейшей упаковке

появляются горизонтальные плоскости m_z , проходящие через слои "г", и центры инверсии - между плоскостями симметрии - в слоях "к", взаимодействие которых с комплексом Р3m1 приведет к гексагональной голоэдрии: Р3m1 + m_z + --> .

B одной из двух возможных шестислойных упаковок - рамзаитовой -

при том же расположении плоскостей симметрии (в слоях "г") центры инверсии оказываются не в слоях "к", а между ними. Однако в результате взаимодействий между элементами симметрии приходим к той же голоэдрической группе .

Симметрия шестислойной плотнейшей упаковки второго типа

характеризуется только плоскостями m_z, что приводит лишь к гемиэдрической ацентричной группе :

Р3m1 + m_z = .

Рассмотрим симметрию одной из семи возможных девятислойных плотнейших упаковок:

Добавление центров инверсии, расположенных в слое "к" и между слоями "гг" к обязательному комплексу Р3m1 даст пр. гр. . Однако количество слоев (9), приходящихся на одну элементарную ячейку, кратное трем, а также их закономерное чередование (А...В...С) через 1/3 вертикальной трансляции указывает на присутствие дополнительного вектора дважды центрированной R-решетки Браве, т.е. на пр. гр. . На присутствие вектора указывает и то, что формула плотнейшей шестислойной упаковки разбивается на три одинаковых по набору букв пакета : ...[кгг - кгг - кгг]...

Аналогичным образом определяется и симметрия одной из 21-слойной плотнейшей упаковки, также описываемая пр. гр. :

Таким образом, убеждаемся в достоинствах каждого из дополняющих друг друга способов обозначения плотнейших упаковок. Если трехбуквенный способ (АВС) позволяет быстро установить слойность упаковки и определить тип решетки Браве, то с помощью двухбуквенного (кг) можно выявить идентичность или различие одинаковых по слойности упаковок, а также выделить независимый пакет слоев каждой упаковки.