Теория симметрии кристаллов

Глава Х. Группы многоцветной симметрии

Рис. 170

Анализ 230 федоровских групп симметрии позволяет выбрать те из них, операции симметрии которых не содержат скольжения вдоль оси Z (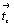). С помощью этих групп можно описать плоские узоры (постройки), составленные из фигур, лежащих в одной плоскости. При этом часть групп (17 полярных групп симметрии) будет описывать односторонние узоры, все фигуры которых обращены к наблюдателю одной лицевой (белой) стороной; другая часть (46 групп) - двусторонние узоры, где фигуры обращены к наблюдателю как лицевой, так и изнаночной (черной) стороной. Поэтому каждой из них можно поставить в соответствие одну из 46 плоских двухцветных (шубниковских) групп (табл. 10, рис. 170, см. цветную вставку).

Например, симметрию узора, изображенного на рис. 170, можно описать с нескольких позиций, придавая цвету различный смысл. С одной стороны, этот узор ( рис. 170, а) иллюстрирует группу антисимметрии pm' a2' , с другой, если считать черный и белый цвет фигур их лицевой и изнаночной сторонами, полученный узор может быть описан федоровской группой ( рис. 170, б). При этом классическим эквивалентом зеркальной плоскости антисимметрии (m' ) станет поворотная ось 2-го порядка (2_у), расположенная на уровне исходных фигур; эквивалентом оси 2_z? - классический центр инверсии (). Придав разноокрашенным фигурам два уровня, отличающиеся на полтрансляции вдоль оси Z (например, белые - на высоте +z, а четные - на высоте , где величина z может принимать любые значения), тот же самый узор можно описать федоровской группой Pca2₁ ( рис. 170, в). В этом случае зеркальная плоскость антисимметрии m' группы pm' a2' станет классической плоскостью скользящего отражения с, ось 2' превратится в классическую 2₁. Классическая плоскость а (плоскость с горизонтальным скольжением) перейдет в новую федоровскую группу Pca2₁ без изменения.

Рис. 171

Очевидно, что элементами симметрии, задающими фигуры на двух уровнях, отличающихся на полтрансляции вдоль оси с элементарной ячейки, будут оси 2₁ , 4₂ , 6₃ , плоскости симметрии c, n и трансляции решеток , , и . При этом такая абстрактная характеристика, как цвет (черно-белая раскраска фигур), в данном случае символизирует два уровня их расположения.

Однако среди 230 федоровских групп симметрии существуют такие, с помощью которых можно описать трехмерные постройки, где симметрически связанные фигуры располагаются на нескольких (более двух!) уровнях - трех, четырех или шести, обеспечиваемых следующими трансляционными элементами симметрии: осями 3₁ , 3₂ , 4₁, 4₃, 6₁, 6₂, 6₄, 6₅, клиноплоскостью d и трансляциями ромбоэдрической ячейки Браве . Вновь, придав в проекции на плоскость чертежа каждому из уровней определенный цвет, получим группы многоцветной симметрии: трех-, четырех- или шестицветной. При этом обозначения цветных групп (G) иногда сопровождаются верхним индексом р (G^(р)), указывающим на количество цветов, кратное порядкам кристаллографических групп - G⁽³⁾, G⁽⁴⁾, G⁽⁶⁾ и т.д. Цвет в данном случае условно выступает в качестве дискретной негеометрической переменной в трехмерном пространстве.

На этой основе Н.В.Беловым и Т.Н.Тарховой в 1956 г. [7, 12, 54] была выдвинута идея многоцветной симметрии. Впервые они вывели 15 двухмерных цветных циклических и кратных от них групп проектированием на плоскость соответствующих федоровских групп, содержащих перечисленные выше трансляционные элементы симметрии: P4₁ , P4₃ , I4₁ , P6₁ , P6₅ , P6₂ , P6₄ , P3₁ , P3₂ , R3, R3m, R3c, I4₁md, I4₁cd и Fdd2 (см. цветную вставку, рис. 171). Работы Н.В.Белова послужили основой вывода остальных пространственных и точечных групп цветной симметрии [37, 43, 45, 46]. Рассмотрим некоторые из мозаик, предложенных Н.В.Беловым.

Рис. 172

Мозаики с симметрией P4₁ и P4_3. Обозначив разным цветом фигуры на 4 уровнях вдоль оси с элементарной ячейки, связанные операциями симметрии винтовых осей 4₁ и 4₃ и спроектированные на плоскость чертежа, получим цветные мозаики, иллюстрирующие соответствующие федоровские группы симметрии - Р4₁ и Р4₃ (см. цветную вставку, рис. 172). Условно принятая последовательность цветов - прямая (желтый (1) - синий (2) - красный (3) - зеленый (4)) и обратная (зеленый - красный - синий - желтый) - укажет направление вращения вокруг осей 4₁ или 4₃ соответственно.

Рис. 173

Приведенные мозаики позволяют проследить все особенности пространственных групп симметрии Р4₁ и Р4₃ : два типа одноименных трансляционно неидентичных винтовых осей (в вершинах и в центре элементарной ячейки) и расположенные на серединах ребер ячейки винтовые оси 2₁ .

Мозаика с симметрией R3. Для иллюстрации группы симметрии R3 необходима трехцветная мозаика (см. цветную вставку, рис. 173, а) с ясно видимыми энантиоморфными осями 3₁ и 3₂, неизбежно сопровождающими в R-решетках поворотные оси 3-го порядка (рис. 173, б).

Рис. 174

Мозаика с симметрией P6₁. Мозаика с симметрией Р6₁ предполагает 6 цветов (6 уровней): красный - белый - синий - желтый - черный - зеленый (см. цветную вставку, рис. 174, а). В центрах шестиугольников расположены оси 6₁ , включающие в себя оси 3₁ и 2₁, взаимодействие которых с горизонтальными трансляциями решетки (каждая по своему закону), вызывает появление указанных осей в различных позициях элементарной ячейки (рис. 174, б).

Мозаики с симметрией I4₁md и Fdd2. В пространственной группе I4₁md ось 4₁ является результатом взаимодействия плоскостей симметрии m и d, при этом алмазная плоскость d обусловливает 4 уровня расположения фигур, т.е. четырехцветную мозаику (см. цветную вставку, рис. 175, а). Хорошо видно чередование энантиоморфных осей 4₁ и 4₃ вдоль горизонтальных ребер элементарной ячейки и осей 2-го порядка в центрах одноцветных квадратов.

Рис. 175

Интересен переход от тетрагональной группы I4₁md = F4₁dm к ромбической Fdd2 путем деформации исходной тетрагональной ячейки вдоль алмазной плоскости d, при которой исчезают зеркальные плоскости m, а следовательно, и оси 4₁ и 4₃ (рис. 175, б). Таким образом, цветные мозаики могут иллюстрировать как определенные федоровские группы, так и цветные плоские группы.

Рис. 176

Цветную симметрию можно показать на 18 точечных группах многоцветной симметрии [37] - 18 беловских группах (классах), проиллю-стрировав их трех-, четырех- или шестицветными фигурами (см. цветную вставку, рис. 176).

Выбрав из 32 точечных групп симметрии 10 групп, пригодных для <зацвечивания>, т.е. групп с осями высшего порядка, без перпендикулярных к ним осей 2, а также без параллельных им зеркальных плоскостей симметрии, делающих <зацвечивание> бессмысленным, -

, pассмотрим возможности их <зацвечивания>. Обязательным цветным элементом симметрии во всех перечисленных группах будет ось высшего порядка: 3⁽³⁾, 4⁽⁴⁾, либо 6⁽ⁿ⁾ = 3 ^.2. Для последней следует рассмотреть два варианта: с простой и цветной осью 2. Поэтому каждая из осей 6-го порядка - поворотная (6), зеркальная () и инверсионная () - может оказаться либо шестерной цветной - 6⁽⁶⁾, ⁽⁶⁾, , либо тройной цветной осью - 6⁽³⁾, ⁽³⁾, ; где 6⁽⁶⁾ = 3' ^.  2' , , ⁽⁶⁾ и 6⁽³⁾ = 3' ^. 2, , ⁽³⁾ . (Штрихи, заимствованные из обозначений эле-ментов антисимметрии, в данном случае указывают на цветные элементы симметрии, показатели степени в скобках - на количество цветов)

Для цветных групп, подчиненных полярной , возможны 4 варианта <зацвечивания> входящих в них элементов симметрии 2-го порядка:

(см. рис. 176). Раскраска групп тетрагональной сингонии, подчиненных точечной , даст две цветные группы: и . Учитывая приведенные выше ограничения, касающиеся элементов симметрии 2-го порядка, из пяти кубических точечных групп симметрии следует исключить классы и 432. Для оставшихся двух классов - 23 и - возможны лишь три варианта цветных групп: 23' , . Однако если в первой из них три координатные оси 2-го порядка (зависимые одна от другой - 2_x ^. 2_y = = 2_z - и связанные между собой осями 3) не могут быть <зацвечены>, то в двух последних координатные плоскости m не зависят одна от другой и поэтому могут быть цветными.

Существуют и некристаллографические точечные цветные группы, где число цветов может быть кратно пяти.

Беловская цветная симметрия послужила основой для разработки различного рода расширений цветных групп симметрии. В частности, помимо выведенных выше 18 цветных точечных групп - беловских классов - были получены пространственные беловские группы, а синтез идей цветной симметрии и кратной антисимметрии привел к понятию цветной антисимметрии, которое, в свою очередь, в дальнейшем получило соответствующее развитие [43, 45, 46]. Таким образом, все новые идеи в учении о симметрии тесно переплетаются, содействуя развитию друг друга, и находят применение при описании свойств и симметрии кристаллов.

Примеры использования шубниковских и цветных групп в кристаллофизике

Рис.177

Группы антисимметрии и цветной симметрии используют при описании некоторых физических свойств кристаллов, например электрических (расположение электрических моментов) или магнитных (упорядоченные структуры, в которых магнитные моменты атомов могут принимать две или несколько ориентаций) [14, 31]. Так, схематично показанные на рис. 177 различные конфигурации магнитных векторов в кристаллических структурах, условно изображенные полярными стрелками, невозможно описать с использованием лишь классической симметрии или антисимметрии. Если за исходную взять точку 1 с вертикально ориентированным магнитным моментом во всех типах изображенных магнитных структур, то на рис. 177, а расположения векторов естественно описываются с помощью операций классической симметрии, т.е. поворотами вокруг оси 6-го порядка. На рис. 177, б каждый правый поворот (против часовой стрелки) на 60^o сопровождается изменением направления магнитного вектора на противоположный поворотом на 180^o , что делает возможным описание данной конфигурации с позиций антисимметрии - с помощью оси 6' . Переход от точки 1 в точку 2 (рис. 177, в) можно осуществить простым поворотом вокруг оси 6. При этом, казалось бы, жестко связанный с точкой магнитный момент (вектор) должен быть ориентированным в точке 2 по внешнему радиусу. Однако его истинное положение по образующей правильного шестиугольника отвечает вектору, подвергшемуся дополнительному преобразованию - повороту на 60^o против часовой стрелки. Многократно повторенные операции - основная и дополнительная (60^o + 60^o ) - приведут к типичной неколлинеарной антиферромагнитной конфигурации. Осуществляя в качестве дополнительного преобразования поворот вектора на 60^o по часовой стрелке (левый поворот), получим коллинеарную ферромагнитную структуру (рис. 177, г). Введя в качестве дополнительного преобразования к классическому повороту на 60^o правый или левый поворот на 120^o , получим антиферромагнитные структуры с другими ориентациями магнитных векторов (рис. 177, д, е).

Вместо магнитного момента материальным точкам пространства можно придавать иные физические характеристики, соответственно сопроводив их другими дополнительными преобразованиями, также несущими определенную физическую нагрузку. Возникающие при этом группы симметрии окажутся изоморфными соответствующим группам, которые можно назвать "цветными", приписав предварительно дополнительным преобразованиям такую абстрактную характеристику, как цвет. Таким образом, группа 6⁽⁶⁾ (рис. 177, в) будет шестицветной, а группа 6⁽³⁾ - трехцветной (ср. с 6' - двухцветной и 6 - одноцветной).