|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
XII.2. Преобразование индексов
плоскостей - индексов узловых сеток - и граней
кристаллов
При переходе от одной координатной системы к
другой, естественно, меняются отрезки,
отсекаемые какой-либо системой атомных
плоскостей на координатных осях, а
следовательно, и символы этих плоскостей. Для
выявления характера изменения индексов
некоторой узловой сетки (hkl), рассчитанных в
исходном координатном репере (X,Y,Z) ограничимся
двухмерным случаем (рис. 210). В качестве примера
возьмем систему плоских узловых сеток (hk0),
разбивающих сторону а элементарного
параллелограмма на 4 части и сторону b - на три
части. Абсолютные величины отрезков (параметров),
отсекаемых ближайшей к началу координат сеткой (hk0)
на осях X и Y, будут соответственно равны p = 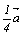 и q = и q =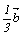 . Отсюда индексы h и k такой
ближайшей к началу координат сетки будут
соответственно равны 4 и 3: (430), где h = . Отсюда индексы h и k такой
ближайшей к началу координат сетки будут
соответственно равны 4 и 3: (430), где h = 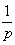 = 4 и k = = 4 и k = 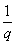 = 3. Обратим внимание на то, что речь
идет не о символе грани, где индексы могут быть
сокращены на общий множитель, а о символе
конкретной узловой сетки, где такое сокращение
невозможно. = 3. Обратим внимание на то, что речь
идет не о символе грани, где индексы могут быть
сокращены на общий множитель, а о символе
конкретной узловой сетки, где такое сокращение
невозможно.
Для вычисления новых индексов (HKL) этой
плоскости в новой системе координат (X' , Y' , Z' )
следует определить, на сколько частей разбивает
система узловых плоскостей единичные отрезки 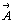 , , 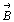 и и 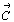 вдоль новых
координатных осей. Из рис. 210 видно,
что единичные векторы вдоль новых
координатных осей. Из рис. 210 видно,
что единичные векторы 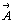 , ,
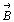 вдоль новых осей X' , Y'
есть векторные суммы единичных векторов вдоль
старых осей: вдоль новых осей X' , Y'
есть векторные суммы единичных векторов вдоль
старых осей:
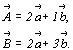
Оказывается, что число отрезков, на которые
рассечен вектор 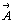 рассматриваемой системой плоскостей со старым
символом (430), равно сумме числа разбиений
векторов
рассматриваемой системой плоскостей со старым
символом (430), равно сумме числа разбиений
векторов 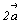 и и 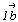 , т.е. равно 2. 4+1.
3 = = 11, так же как число разбиений вектора , т.е. равно 2. 4+1.
3 = = 11, так же как число разбиений вектора 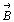 равно 2. 4+3. 3 =
17. Таким образом, числа 11 и 17 не что иное, как новые
индексы H и K рассматриваемой системы
плоскостей, соответствующие новым осям X' и Y' : равно 2. 4+3. 3 =
17. Таким образом, числа 11 и 17 не что иное, как новые
индексы H и K рассматриваемой системы
плоскостей, соответствующие новым осям X' и Y' :
H = 2 . 4 + 1 . 3 = 11, K = 2 .
4 + 3 . 3 = 17.
Как видим, каждая из новых векторных единиц
разбита на количество отрезков, равное сумме
разбиений его проекций по осям X и Y исходного
координатного репера.
В общем случае в новой системе координат
единичный вектор 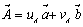 ,
следовательно, индекс Н = uAh + vAk, а
так как ,
следовательно, индекс Н = uAh + vAk, а
так как 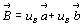 , то К = uBh
+ vBk. , то К = uBh
+ vBk.
Таким образом, для трехмерного случая
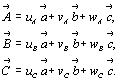
Отсюда преобразование индексов
плоскостей запишется системой уравнений с
коэффициентами, полученными для преобразования
параметров решетки:
Н = uAh + vAk + wAl,
K = uBh + vBk+ wBl, (6)
L = uCh + vCk + wCl
и соответствующей матрицей: 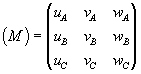 . .
Обратим внимание на то, что матрица
преобразования индексов плоскости (узловой
сетки, грани) совпадает с матрицей (1)
преобразования координатных осей, т.е.
преобразование символов граней тоже отвечает
ковариантному закону:
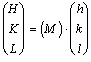 и и 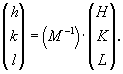
Таким образом, при переходе к новому
координатному реперу можно легко вычислить и
новые индексы любой плоскости (hkl), придав
конкретные цифровые значения коэффициентам u, v,
w матрицы преобразования осей (2).
Иногда вследствие неоднозначного выбора
координатной системы одним и тем же граням
какого-либо кристалла разными авторами
приписываются различные символы. В этом случае
задачу преобразования символа любой узловой
плоскости (грани) в одной координатной системе к
символу этой же плоскости (грани) в другой
системе легко решить, найдя матрицу
преобразования (М) от одной координатной
системы к другой. Для этого следует подставить
частные значения индексов (H,K,L в одной
координатной системе и h,k,l - в другой)
ограниченного числа плоскостей в систему
уравнений (6) и решить их относительно
коэффициентов u,v,w.
Например, пусть символы (hkl) трех плоскостей
(граней I, II и III) в старом координатном репере: (110),
(210) и (001) приобрели в новой системе координат
значения (HKL) соответственно (230), (340) и (001) [22].
Значения коэффициентов u, v, w легко вычислить,
решив систему уравнений (6). Подставив значения
индексов (h,k,l) в уравнение
H = uA . h + vA . k
+ wA . l для всех трех исходных
граней (I, II, III), получим:
для плоскости I HI = uA . 1
+ vA . 1 + wA . 0 = 2 ;
uA + vA = 2,
для плоскости II HII = uA . 2
+ vA . 1 + wA . 0 = 3 ;
2uA + vA = 3,
для плоскости III HIII = uA . 0
+ vA . 0 + wA . 1 = 0
; wA = 0.
Откуда найдем значения uA = 1, vA = 1, wA
= 0.
Для того чтобы найти коэффициенты uB ,vB
,wB, подставим зна-чения индексов (h,k,l)
во второе уравнение (6): K = uB . h +
vB . k + wB . l:
для плоскости I KI = uB . 1
+ vB . 1 + wB . 0 = 3 ;
uB + vB = 3,
для плоскости II KII = uB . 2
+ vB . 1 + wB . 0 = 4 ;
2uB + vB = 4,
для плоскости III KIII = uB . 0
+ vB . 0 + wB . 1 = 0
; wB = 0,
откуда uB = 1, vB = 2, wB = 0.
Решение 3-й системы уравнений (6): L = uC .
h + vC . k + wC . l:
для плоскости I LI = uC . 1
+ vC . 1 + wC . 0 = 0 ;
uC + vC = 0,
для плоскости II LII = uC . 2
+ vC . 1 + wC . 0 = 0 ;
2uC + vC = 0,
для плоскости III LIII = uC . 0
+ vC . 0 + wC . 1 = 1
; wC = 1,
даст значения uC = 0, vC = 0, wC = 1.
Записав найденные значения u, v, w в виде
таблицы, получим искомую матрицу преобразования
символов граней:
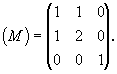
Элементы такой матрицы, будучи подставлены в
качестве коэффициентов в уравнения (6), дадут
общий закон, определяющий преобразование
индексов любых плоскостей, атомных сеток или
граней какого-либо кристалла при заданном
преобразовании координатных осей:
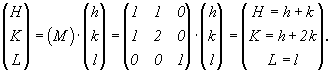
|

