|
Авторы: Ю.К.Егоров-Тисменко, Г.П.Литвинская
( Под редакцией В.С.Урусова)
|
Содержание |
Глава XII. Преобразования
кристаллографических координатных систем
Решение многих кристаллографических задач
связано с переходом от одной установки
кристаллического многогранника или
кристаллической структуры к другой, т.е. с
преобразованием их координатных систем. С одной
стороны, полное отсутствие или недостаточное
количество особых направлений в группах
триклинной и моноклинной сингоний и некоторых
группах сингоний средней категории допускает
неоднозначность выбора ячейки Браве, с другой -
многие исследователи , отдавая дань традициям,
либо из кристаллохимических соображений иногда
приводят описания кристаллических структур в
нестандартном аспекте, пренебрегая, таким
образом, требованиями минимального объема
ячейки. Например, описание кристаллов или их
структур гексагональной сингонии часто
приводится в миллеровском, а не в гексагональном
- R-аспекте и т.п. А так как каждая координатная
система определяется направлением и величиной
координатных трансляций (параметров ячейки),
выбранных в соответствии с симметрией решетки,
переход от одного координатного репера к другому
подразумевает вычисление как параметров новой
ячейки, а следовательно, и новых координат
атомов, так и символов атомных плоскостей и
направлений [28, 29, 32].
XII.1. Преобразование параметров
решетки
Рассмотрим общий случай перехода от "старого"
- исходного - координатного репера,
характеризующегося единичными трансляционными
векторами 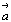 , , 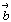 и и 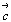 вдоль соответствующих координатных
направлений X, Y и Z, к "новому" реперу с
единичными векторами вдоль соответствующих координатных
направлений X, Y и Z, к "новому" реперу с
единичными векторами 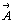 , , 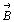 и и 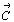 вдоль новых координатах осей X' , Y' и Z' (при
условии их общего начала) (рис. 208). вдоль новых координатах осей X' , Y' и Z' (при
условии их общего начала) (рис. 208).
Выразив параметры 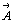 , , 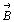 и и 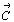 вдоль новых координатных осей как
векторные суммы старых вдоль новых координатных осей как
векторные суммы старых 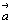 , ,
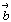 и и 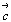 , получим систему уравнений, общая форма
которых всегда одинакова для любого
преобразования осей: , получим систему уравнений, общая форма
которых всегда одинакова для любого
преобразования осей:
 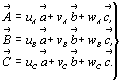 (1) (1)
Поскольку индивидуальный характер каждого
частного преобразования определяется только
коэффициентами (u, v, w) при векторах (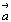 , , 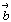 , , 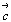 ) "старого"
координатного репера, то систему
рассматриваемых уравнений можно записать
сокращенно в виде составленной из этих
коэффициентов таблицы, называемой матрицей
преобразования: ) "старого"
координатного репера, то систему
рассматриваемых уравнений можно записать
сокращенно в виде составленной из этих
коэффициентов таблицы, называемой матрицей
преобразования:
(M)ст --> нов =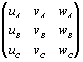 = uA vA wA /
uB vB wB / uC vC wC. (2) = uA vA wA /
uB vB wB / uC vC wC. (2)
Переход от нового координатного репера (X' , Y' , Z'
) к старому (X, Y, Z) также можно выразить системой
уравнений, связывающей единичные векторы новой (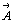 , , 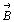 , , 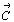 ) и старой ( ) и старой (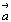 , , 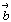 , , 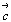 ) систем: ) систем:
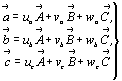 (3) (3)
и соответствующей матрицей:
(М-1)нов--> ст = 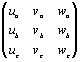 = ua va wa
/ ub vb wb / uc vc wc . = ua va wa
/ ub vb wb / uc vc wc .
Обратим внимание на то, что каждая строка
полученных матриц прямого и обратного переходов
выражает миллеровский символ соответствующей
координатной оси: в первом случае [ uAvAwA
] - символ новой оси X' , [ uB vB wB
] - оси Y' , [ uC vC wC ] - оси Z' в
старой координатной системе, и во втором случае -
[ ua va wa ] - символ старой оси X,
[ub vb wb ] - оси Y и [uc vc
wc ] - оси Z в новой координатной системе,
так как коэффициенты u, v и w не что иное,
как координаты точки, расположенной на
соответствующей координатной оси, выраженные в
долях параметров исходной ячейки. Отметим, что
взаимнообратные матрицы (М) и (М-1)
при перемножении (см. с. 27) дают единичную матрицу
- матрицу идентичного преобразования:
(М) . (M-1) = 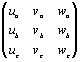 . .
B общем случае (М1) . (М2)  (М2)
. (М1). (М2)
. (М1).
Для того чтобы получить единичные векторы
новой координатной системы (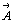 , , 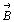 , , 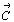 ), т.е. параметры новой ячейки,
следует на матрицу соответствующего
преобразования (М)ст--> нов умножить
одностолбцовую матрицу, составленную из
параметров старой ячейки - векторных единиц
старой координатной системы: ), т.е. параметры новой ячейки,
следует на матрицу соответствующего
преобразования (М)ст--> нов умножить
одностолбцовую матрицу, составленную из
параметров старой ячейки - векторных единиц
старой координатной системы:
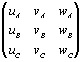 . .
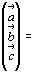 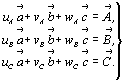 (4) (4)
Таким же образом можно рассчитать параметры 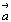 , , 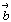 и и 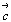 по матрице
обратного преобразования (М-1): по матрице
обратного преобразования (М-1):
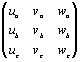 . .
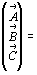 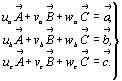 (5) (5)
Закон, по которому преобразуются параметры
элементарной ячейки, носит название ковариантного.
Абсолютное значение параметров 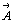 , , 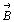 , , 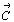 или или 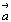 , , 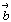 , , 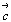 получают извлечением квадратного
корня из скалярного произведения каждого
вектора на самого себя: получают извлечением квадратного
корня из скалярного произведения каждого
вектора на самого себя:
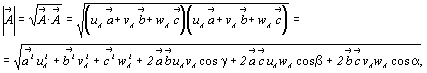
где 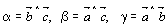 - углы между
осями X, Y, Z старой координатной системы.
Аналогично вычисляются значения параметров - углы между
осями X, Y, Z старой координатной системы.
Аналогично вычисляются значения параметров 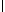 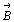 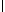 и и 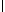 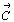 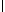 . .
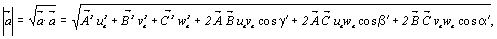
где 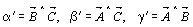 - углы между
осями X' , Y' , Z' новой координатной системы. - углы между
осями X' , Y' , Z' новой координатной системы.
Воспользовавшись зависимостью
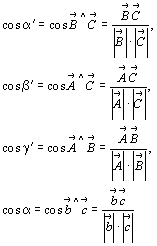
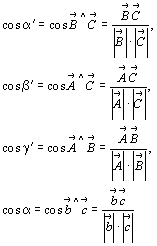
и т.д., можно вычислить и углы между осями:
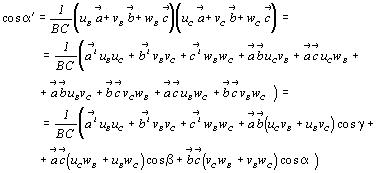
и т.д.
Если (М1) - матрица
преобразования параметров от первой
координатной системы ко второй, а (М2) -
от второй к третьей, то матрица преобразования от
первой системы к третьей (М3) выразится
произведением исходных матриц: (М1).
(М2) = (М3).
В качестве примера (рис. 209)
рассмотрим преобразование старой координатной
системы (X,Y,Z) в новую (X' , Y' , Z' ) с единичными
векторами 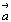 , , 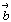 , , 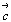 и и 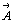 , , 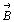 , , 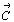 соответственно при условии единого их начала и
совпадения векторных единиц вдоль координатных
направлений Z и Z' , т.е.
соответственно при условии единого их начала и
совпадения векторных единиц вдоль координатных
направлений Z и Z' , т.е. 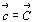 .
Выразив единичные векторы как векторные суммы
старых параметров, получим систему уравнений .
Выразив единичные векторы как векторные суммы
старых параметров, получим систему уравнений
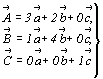
и запишем ее в матричной форме:
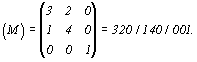
Нетрудно убедиться в том, что каждая строка
полученной матрицы представляет собой
координаты первого узла (1-й точки) на
соответствующей новой оси в единицах исходной
(старой) координатной системы, отношения которых
(координат) дают миллеровские символы новых
координатных осей X' , Y' , Z' в старой системе: [320],
[140] и [001] соответственно.
Матрицу обратного преобразования (М-1)
от новой координатной системы к старой в данном
случае удобно получить графически 1
(см. рис. 209). Для этого из
построенных треугольников OPR и OST, стороны
которых выражены целочисленными значениями как
старых, так и новых параметров, получим:
для D OPR - 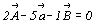 , откуда , откуда 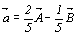 , ,
для D OST - 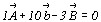 , откуда , откуда 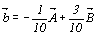 , ,
при этом 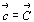 . .
Таким образом, матрица обратного
преобразования
(М-1)нов--> ст будет иметь вид:
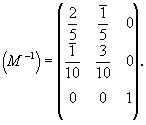
Перемножение полученных взаимно
обратных матриц (М) и (М-1), как и
следовало ожидать, приведет к единичной матрице 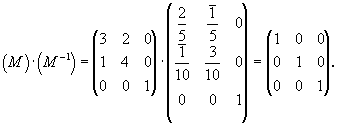
Далее, подставив значения исходных единичных
векторов в выражения (4) и (5), получим единичные
векторы той или иной искомой координатной
системы.
|

